Extrasitzung

Einfach Textdateien speichern

Daten

library(ggplot2)

d <- as.data.frame(msleep) # from ggplot2 package
head(d)

##                         name      genus  vore        order conservation
## 1                    Cheetah   Acinonyx carni    Carnivora           lc
## 2                 Owl monkey      Aotus  omni     Primates         <NA>
## 3            Mountain beaver Aplodontia herbi     Rodentia           nt
## 4 Greater short-tailed shrew    Blarina  omni Soricomorpha           lc
## 5                        Cow        Bos herbi Artiodactyla domesticated
## 6           Three-toed sloth   Bradypus herbi       Pilosa         <NA>
##   sleep_total sleep_rem sleep_cycle awake brainwt  bodywt
## 1        12.1        NA          NA  11.9      NA  50.000
## 2        17.0       1.8          NA   7.0 0.01550   0.480
## 3        14.4       2.4          NA   9.6      NA   1.350
## 4        14.9       2.3     0.13333   9.1 0.00029   0.019
## 5         4.0       0.7     0.66667  20.0 0.42300 600.000
## 6        14.4       2.2     0.76667   9.6      NA   3.850

sink

Auch im Arbeitsverzeichnis (\(\rightarrow\) getwd)
cat erzeugt den Textstring in seinem Argument auch in der Textdatei, nützlich für Titel, wenn mehrere Berechnungen in dieselbe Datei sollen
\n erzeugt einen Zeilenumbruch
Mit with erspart man sich ein kleines bisschen Schreibarbeit, weil man den Datensatz selbst nicht immer wieder innerhalb der Funktion eingeben muss
Wichtig: sink immer mit sink beenden, wenn die Textdatei alle Infos enthält, die man abspeichern wollte

library(psych)
sink("descriptive_stats.txt")
cat("\n\n###################################################################")

with(d,
  describeBy(price, cut))

cat("\n\n###################################################################")
sink()

Funktionen aus dem tidyverse

Tidyverse

https://www.tidyverse.org

install.packages("tidyverse")

library(tidyverse)

Funktionen, die man kennen sollte

mutate() # spalten erstellen oder verändern
summarise() # mehrere werte auf einen reduzieren (zB mean)
group_by() # datenblatt gruppieren (wie by() )
%>% # "pipe"

Pipe %>%

https://twitter.com/andrewheiss/status/1173743447171354624

Beispiele

# Spalte für Faktor Issueness anlegen
d <- mutate(d, issue = case_when(
  str_detect(d$V8, "_at") ~ "at-issue",
  str_detect(d$V8, "_non") ~ "non-at-issue"))

# Spalten zu Faktoren konvertieren
d <- mutate_at(d,
  c("issue", "trigger", "itemid", "lex"),
  funs(factor(.)))

# neue Spalte und Faktoren mit Pipes
d <- d %>%
  mutate(issue = case_when(
    str_detect(V8, "_at") ~ "at-issue",
    str_detect(V8, "_non") ~ "non-at-issue")) %>%
  mutate_at(c("issue", "trigger", "itemid", "lex"),
    funs(factor(.)))

Weitere Beispiele

Mit dem altbekannten Diamantendatenset:

d <- diamonds
head(d)

##   carat       cut color clarity depth table price    x    y    z
## 1  0.23     Ideal     E     SI2  61.5    55   326 3.95 3.98 2.43
## 2  0.21   Premium     E     SI1  59.8    61   326 3.89 3.84 2.31
## 3  0.23      Good     E     VS1  56.9    65   327 4.05 4.07 2.31
## 4  0.29   Premium     I     VS2  62.4    58   334 4.20 4.23 2.63
## 5  0.31      Good     J     SI2  63.3    58   335 4.34 4.35 2.75
## 6  0.24 Very Good     J    VVS2  62.8    57   336 3.94 3.96 2.48

Vorkommen zählen

# reihen zählen und nach color und cut aufspalten
d %>% count(color, cut) %>%
  head

## # A tibble: 6 x 3
##   color cut           n
##   <ord> <ord>     <int>
## 1 D     Fair        163
## 2 D     Good        662
## 3 D     Very Good  1513
## 4 D     Premium    1603
## 5 D     Ideal      2834
## 6 E     Fair        224

Zählen und Sortieren

d %>% count(color, cut) %>%
  arrange(n) %>%
  head()

## # A tibble: 6 x 3
##   color cut       n
##   <ord> <ord> <int>
## 1 J     Fair    119
## 2 D     Fair    163
## 3 I     Fair    175
## 4 E     Fair    224
## 5 H     Fair    303
## 6 J     Good    307

Sortieren und Spalten auswählen

d %>% arrange(desc(price)) %>%
  dplyr::select(price, carat, color, cut) %>%
  head()

##   price carat color       cut
## 1 18823  2.29     I   Premium
## 2 18818  2.00     G Very Good
## 3 18806  1.51     G     Ideal
## 4 18804  2.07     G     Ideal
## 5 18803  2.00     H Very Good
## 6 18797  2.29     I   Premium

Gruppieren und rechnen

d %>% group_by(color) %>%
  summarise(mprice = mean(price),
    medprice = median(price))

## # A tibble: 7 x 3
##   color mprice medprice
##   <ord>  <dbl>    <dbl>
## 1 D      3170.    1838 
## 2 E      3077.    1739 
## 3 F      3725.    2344.
## 4 G      3999.    2242 
## 5 H      4487.    3460 
## 6 I      5092.    3730 
## 7 J      5324.    4234

Gruppieren, berechnen, filtern

# nach schliff gruppieren
# spalte mit mittlerem preis hinzufügen
# und maximale verkaufspreise anzeigen lassen
d %>% group_by(cut) %>%
  mutate(mprice = mean(price)) %>%
  filter(price == max(price))

## # A tibble: 5 x 11
## # Groups:   cut [5]
##   carat cut       color clarity depth table price     x     y     z mprice
##   <dbl> <ord>     <ord> <ord>   <dbl> <dbl> <int> <dbl> <dbl> <dbl>  <dbl>
## 1  2.01 Fair      G     SI1      70.6    64 18574  7.43  6.64  4.69  4359.
## 2  2.8  Good      G     SI2      63.8    58 18788  8.9   8.85  0     3929.
## 3  1.51 Ideal     G     IF       61.7    55 18806  7.37  7.41  4.56  3458.
## 4  2    Very Good G     SI1      63.5    56 18818  7.9   7.97  5.04  3982.
## 5  2.29 Premium   I     VS2      60.8    60 18823  8.5   8.47  5.16  4584.

Gruppenkorrelationen plotten

# nach farbe gruppieren
# und korrelation zwischen preis und gewicht berechnen
# und plotten
d %>% group_by(color) %>%
  summarise(price_carat_cor = cor(price, carat)) %>%
  ggplot(aes(color, price_carat_cor, group = 1)) +
  geom_path()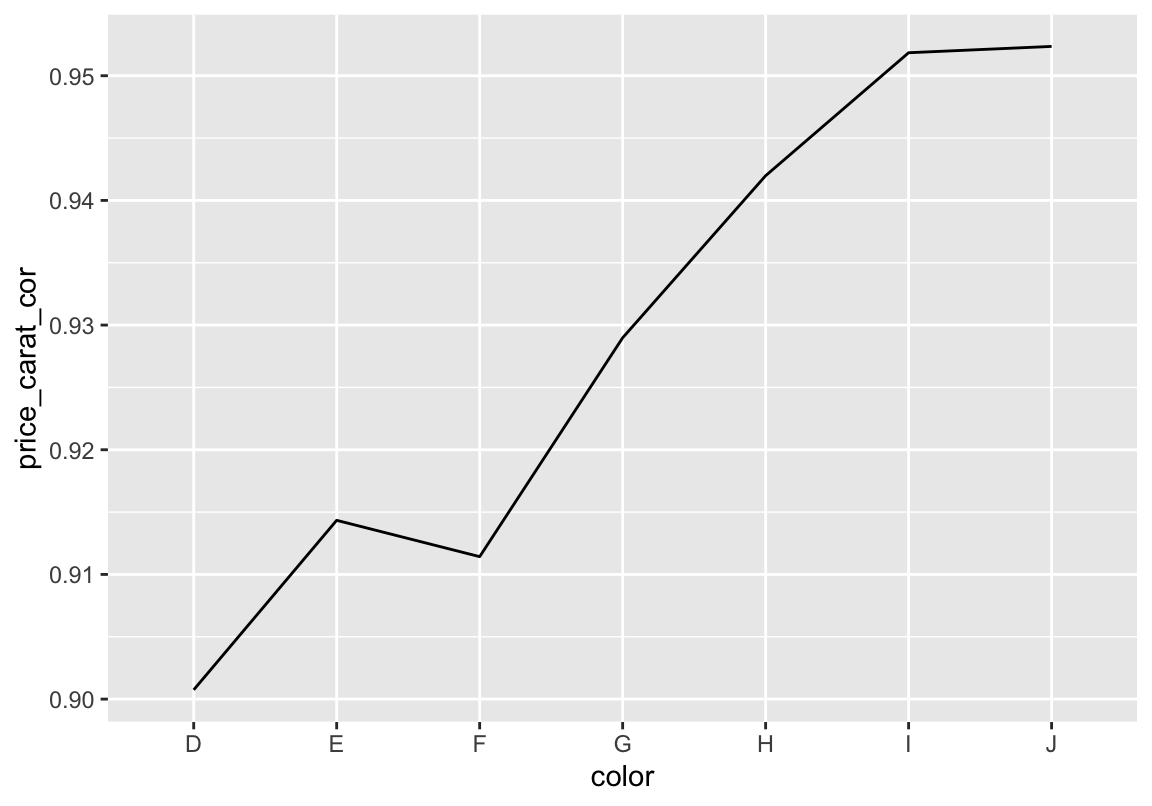

Filtern und plotten

# nur zeilen mit preis > 15000 und schliff == Fair
# im plot darstellen
d %>% filter(price > 15000, cut == "Fair") %>%
  ggplot(aes(carat, price)) +
  geom_point()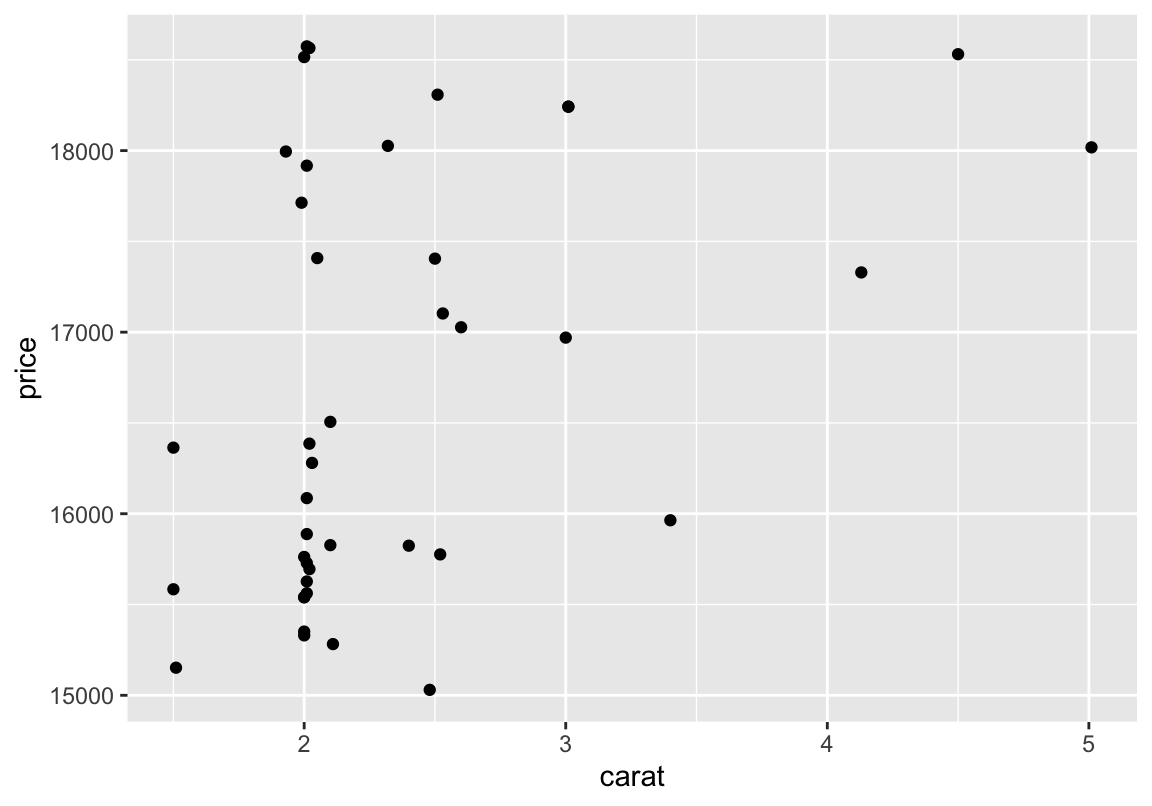

Ein Tutorial

vignette("dplyr")

Speed-Up

Bei größeren Datensätzen (Korpusdaten, EGG, Eye-Tracking) kann es vorkommen, dass die inhärenten Funktionen von R und dem tidyverse zu langsam sind. Wem eine solche Situation häufiger unterkommt, sollte es sich überlegen, die unteren beiden Pakete in seinen Workflow zu integrieren. Beide bieten tidyverse-Syntax mit der Geschwindigkeit von data.table, einem Paket, das zwar wesentlich schneller als andere Lösungen ist, aber einiges an Komplexität mit sich bringt.

For-Loops

Loops

# ausgabe aller geraden zahlen zwischen 1 und 15
for (i in 1:15) { # 1:15 = zahlenreihe 1 bis 15
  if (i %% 2) { # wenn die jeweilige zahl durch 2 teilbar ist, ...
    next} # dann gehe zum nächsten Schritt und
  print(i) # gib sie aus
}

## [1] 2
## [1] 4
## [1] 6
## [1] 8
## [1] 10
## [1] 12
## [1] 14

Loops

# summe: x_1 + x_2 + ... + x_n
my.sum <- function(vector) {
  sum <- 0 # ist nötig, damit wir immer wieder neu bei
  # null beginnen, wenn wir die funktion nochmal benutzen wollen
  for (i in vector) {sum <- sum + i
  }
  sum
}

a <- c(1, 2, 3, 4, 5, 6)
my.sum(a)

## [1] 21

sum(a)

## [1] 21

my.sum(c(1, 2, 3, 4, 5, 6))

## [1] 21

Übung

Schreibe eine Funktion “my.mean”, die den Mittelwert eines Vektors berechnet
Schreibe eine Funktion “my.var”, die die Varianz eines Vektors berechnet

Lösungen

Schreibe eine Funktion “my.mean”, die den Mittelwert eines Vektors berechnet

# mittelwert: (x_1 + x_2 + ... + x_n)/n
my.mean <- function(vector) {
  sum <- 0 # wie oben
  for (i in vector) {
    sum <- sum + i
  }
  sum / length(vector)
}
a <- c(1, 2, 3, 4, 5, 6)
my.mean(a) == mean(a)

## [1] TRUE

my.mean(a)

## [1] 3.5

Lösungen

Schreibe eine Funktion “my.var”, die die Varianz eines Vektors berechnet

# varianz:
# ((x_1-x_mittelwert)+(x_n-x_mittelwert) ... + (x_n-x_mittelwert))/n
my.var <- function(vector) {
  sum <- 0
  meanie <- my.mean(vector)
  for (i in vector) {
    sum <- sum + (i - meanie)^2
  }
  sum / (length(vector) - 1)
}
my.var(a) == var(a)

## [1] TRUE

my.var(a)

## [1] 3.5

Funktionen, die das Coden erleichtern

Daten

d <- InsectSprays
head(d)

##   count spray
## 1    10     A
## 2     7     A
## 3    20     A
## 4    14     A
## 5    14     A
## 6    12     A

str(d)

## 'data.frame':    72 obs. of  2 variables:
##  $ count: num  10 7 20 14 14 12 10 23 17 20 ...
##  $ spray: Factor w/ 6 levels "A","B","C","D",..: 1 1 1 1 1 1 1 1 1 1 ...

by()

by(d$count, d$spray, mean)

## d$spray: A
## [1] 14.5
## ------------------------------------------------------------ 
## d$spray: B
## [1] 15.333
## ------------------------------------------------------------ 
## d$spray: C
## [1] 2.0833
## ------------------------------------------------------------ 
## d$spray: D
## [1] 4.9167
## ------------------------------------------------------------ 
## d$spray: E
## [1] 3.5
## ------------------------------------------------------------ 
## d$spray: F
## [1] 16.667

with()

Struktur:

with(Variable, Befehl/Funktion)

Der Befehl/die Funktion innerhalb von within wird mit der angegebenen Variable durchgeführt

with()

Hier die Daten, mit denen ich die Funktionsweise von with illustrieren werde:

head(ToothGrowth)

##    len supp dose
## 1  4.2   VC  0.5
## 2 11.5   VC  0.5
## 3  7.3   VC  0.5
## 4  5.8   VC  0.5
## 5  6.4   VC  0.5
## 6 10.0   VC  0.5

str(ToothGrowth)

## 'data.frame':    60 obs. of  3 variables:
##  $ len : num  4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
##  $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
##  $ dose: num  0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...

with()

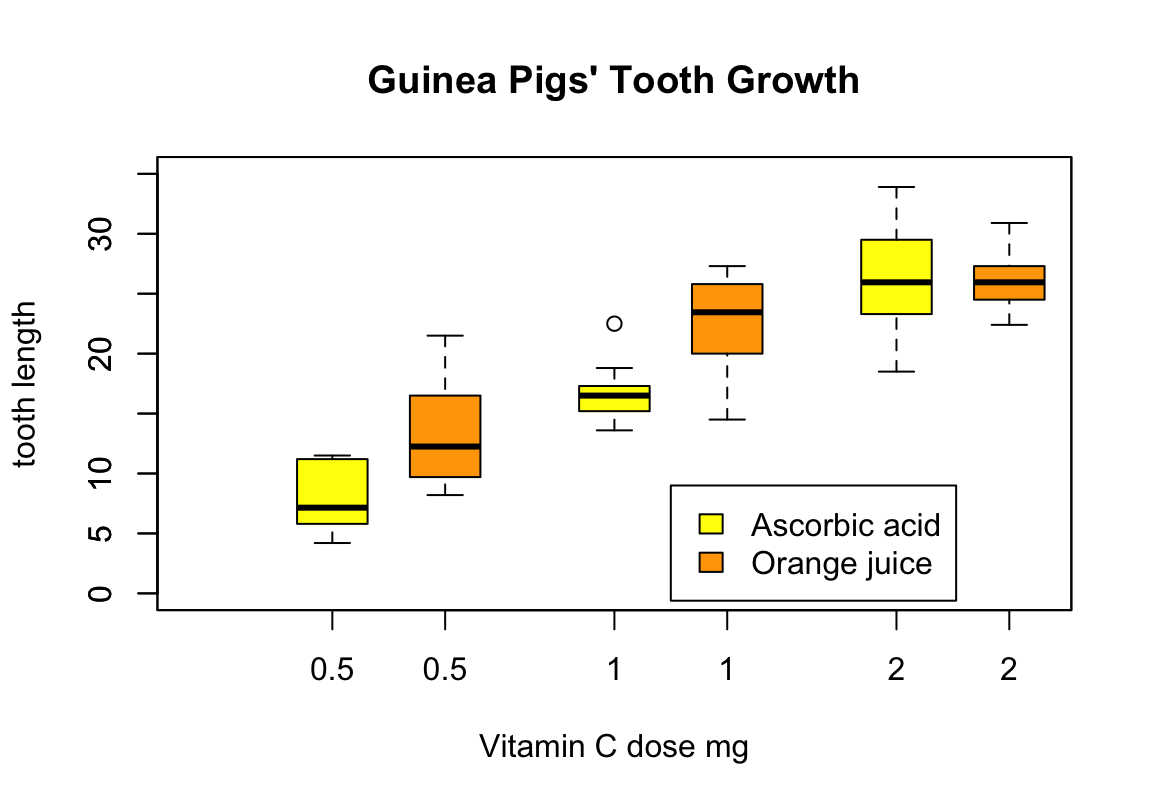
with(ToothGrowth, {
  boxplot(len ~ dose, boxwex = 0.25, at = 1:3 - 0.2,
    subset = (supp == "VC"), col = "yellow",
    main = "Guinea Pigs' Tooth Growth",
    xlab = "Vitamin C dose mg",
    ylab = "tooth length", ylim = c(0, 35))
  boxplot(len ~ dose, add = TRUE, boxwex = 0.25, at = 1:3 + 0.2,
    subset = supp == "OJ", col = "orange")
  legend(2, 9, c("Ascorbic acid", "Orange juice"),
    fill = c("yellow", "orange"))
})

attach()

Alle folgenden Befehle werden mit der angegebenen Variable ausgeführt
Eignet sich, wenn mit wenigen Tabellen/Variablen gleichzeitig gearbeitet wird
Eine Variable, die mit attach ausgewählt wurde, kann mit detach wieder entfernt werden, wenn beispielsweise eine neue Variable verwendet werden soll
Warnung: Google sagt:

Don’t use attach() The possibilities for creating errors when using attach() are numerous.

attach(d)
mean(count)

## [1] 9.5

sd(count)

## [1] 7.2033

median(count)

## [1] 7

mad(count, constant = 1)

## [1] 5

detach(d)

apply()-Familie

tapply(Vektorvariable/Spaltenvariable, INDEX = Vektorvariable/Spalte, Befehl)

für Tabellen/Data-frames
Als zweites Argument muss eine Spalte angegeben werden, nach deren Inhalt die Funktion ausgeführt wird
- Es werden quasi Subsets nach dem Inhalt der angegebenen Spalte erstellt, über die dann einzeln der Befehl angewandt wird.
Alternative Befehle: sapply, lapply

apply()-Familie

# Berechnet Mittelwert und Median der Insektenanzahl
# für den jeweiligen Typ von Insektenspray
tapply(d$count, d$spray, mean)

##       A       B       C       D       E       F 
## 14.5000 15.3333  2.0833  4.9167  3.5000 16.6667

tapply(d$count, d$spray, median)

##    A    B    C    D    E    F 
## 14.0 16.5  1.5  5.0  3.0 15.0

Unterschied by() und tapply()

Janitor-Paket

Installieren und laden

install.packages("janitor")

library(janitor)

Bessere Häufigkeitstabellen

Alternative zu table
Gibt Ergebnisse als data frame aus

d <- diamonds

tab <- tabyl(d, color, cut)
tab # absolute Häufigkeiten

##  color Fair Good Very Good Premium Ideal
##      D  163  662      1513    1603  2834
##      E  224  933      2400    2337  3903
##      F  312  909      2164    2331  3826
##      G  314  871      2299    2924  4884
##      H  303  702      1824    2360  3115
##      I  175  522      1204    1428  2093
##      J  119  307       678     808   896

adorn_percentages(tab, denominator = "row") # relative Häufigkeiten

##  color     Fair     Good Very Good Premium   Ideal
##      D 0.024059 0.097712   0.22332 0.23661 0.41830
##      E 0.022864 0.095233   0.24497 0.23854 0.39839
##      F 0.032698 0.095263   0.22679 0.24429 0.40096
##      G 0.027807 0.077134   0.20360 0.25894 0.43252
##      H 0.036488 0.084538   0.21965 0.28420 0.37512
##      I 0.032276 0.096274   0.22206 0.26337 0.38602
##      J 0.042379 0.109330   0.24145 0.28775 0.31909

Bessere Häufigkeitstabellen

denominator-Argument verändert, wie Häufigkeiten berechnet werden
adorn_pct_formatting: *100 plus %
zusätzlich möglich: adorn_totals

adorn_pct_formatting(adorn_percentages(tab, denominator = "col"))

##  color  Fair  Good Very Good Premium Ideal
##      D 10.1% 13.5%     12.5%   11.6% 13.2%
##      E 13.9% 19.0%     19.9%   16.9% 18.1%
##      F 19.4% 18.5%     17.9%   16.9% 17.8%
##      G 19.5% 17.8%     19.0%   21.2% 22.7%
##      H 18.8% 14.3%     15.1%   17.1% 14.5%
##      I 10.9% 10.6%     10.0%   10.4%  9.7%
##      J  7.4%  6.3%      5.6%    5.9%  4.2%

adorn_pct_formatting(adorn_percentages(tab, denominator = "all"))

##  color Fair Good Very Good Premium Ideal
##      D 0.3% 1.2%      2.8%    3.0%  5.3%
##      E 0.4% 1.7%      4.4%    4.3%  7.2%
##      F 0.6% 1.7%      4.0%    4.3%  7.1%
##      G 0.6% 1.6%      4.3%    5.4%  9.1%
##      H 0.6% 1.3%      3.4%    4.4%  5.8%
##      I 0.3% 1.0%      2.2%    2.6%  3.9%
##      J 0.2% 0.6%      1.3%    1.5%  1.7%

Leere Zeilen und Spalten entfernen

q <- data.frame(v1 = c(1, NA, 3),
  v2 = c(NA, NA, NA),
  v3 = c("a", NA, "b"))
q

##   v1 v2   v3
## 1  1 NA    a
## 2 NA NA <NA>
## 3  3 NA    b

remove_empty(q, c("rows", "cols"))

##   v1 v3
## 1  1  a
## 3  3  b

Spalten mit konstanten Werten entfernen

(a <- data.frame(good = 1:3, boring = "the same"))

##   good   boring
## 1    1 the same
## 2    2 the same
## 3    3 the same

remove_constant(a)

##   good
## 1    1
## 2    2
## 3    3

clean_names()

# Create a data.frame with dirty names
test_df <- as.data.frame(matrix(ncol = 6))
names(test_df) <- c("firstName", "ábc@!*", "% successful (2009)",
  "REPEAT VALUE", "REPEAT VALUE", "")
test_df

##   firstName ábc@!* % successful (2009) REPEAT VALUE REPEAT VALUE   
## 1        NA     NA                  NA           NA           NA NA

clean_names(test_df)

##   first_name abc percent_successful_2009 repeat_value repeat_value_2  x
## 1         NA  NA                      NA           NA             NA NA

Automatische Tabellen mit gtsummary

library(gtsummary)
options(
  gtsummary.add_p.test.continuous_by2 = "t.test",
  gtsummary.add_p.test.continuous = "aov"
)
d <- diamonds
sum_tbl <- d %>%
  select(price, cut, carat) %>%
  mutate(cut = factor(cut, ordered = F)) %>%
  filter(cut %in% c("Premium", "Fair", "Good")) %>%
  droplevels() %>%
  tbl_summary(by = cut,
    statistic = list(all_continuous() ~ "{mean} ({sd})"),
    label = list(carat ~ "Carat",
      price ~ "Price")) %>%
  add_p()

Automatische Tabellen

sum_tbl

Characteristic	Fair, N = 1610¹	Good, N = 4906¹	Premium, N = 13791¹	p-value²
Price	4359 (3560)	3929 (3682)	4584 (4349)	<0.001
Carat	1.05 (0.52)	0.85 (0.45)	0.89 (0.52)	<0.001
¹ Statistics presented: mean (SD) ² Statistical tests performed: One-way ANOVA

Characteristic

Fair, N = 1610¹

Good, N = 4906¹

Premium, N = 13791¹

p-value²

Price

4359 (3560)

3929 (3682)

4584 (4349)

<0.001

Carat

1.05 (0.52)

0.85 (0.45)

0.89 (0.52)

<0.001

¹ Statistics presented: mean (SD)

² Statistical tests performed: One-way ANOVA

`correlation`-Paket

library(correlation)
d %>%
  select(price, carat, depth) %>%
  correlation()

## Parameter1 | Parameter2 |     r |         95% CI |      t |    df |      p |  Method | n_Obs
## --------------------------------------------------------------------------------------------
## price      |      carat |  0.92 | [ 0.92,  0.92] | 551.41 | 53938 | < .001 | Pearson | 53940
## price      |      depth | -0.01 | [-0.02,  0.00] |  -2.47 | 53938 | 0.013  | Pearson | 53940
## carat      |      depth |  0.03 | [ 0.02,  0.04] |   6.56 | 53938 | < .001 | Pearson | 53940

Automatische Berichte

`report`-Paket

Hier zu finden: https://github.com/easystats/report

install.packages("devtools")
devtools::install_github("easystats/report")

library(report)

Dataframes

d <- diamonds
d %>%
  select(price, carat, cut) %>%
  report_sample()

## # Descriptive Statistics
## 
## Characteristic     |         Summary
## ------------------------------------
## Mean price (SD)    | 3932.8 (3989.4)
## Mean carat (SD)    |       0.8 (0.5)
## cut [Fair], %      |             3.0
## cut [Good], %      |             9.1
## cut [Very Good], % |            22.4
## cut [Premium], %   |            25.6
## cut [Ideal], %     |            40.0

report_sample(d, group_by = "cut", select = c("price", "carat"))

## # Descriptive Statistics
## 
## Characteristic  |   Fair (n=1610) |   Good (n=4906) | Very Good (n=12082) | Premium (n=13791) | Ideal (n=21551) |           Total
## ---------------------------------------------------------------------------------------------------------------------------------
## Mean price (SD) | 4358.8 (3560.4) | 3928.9 (3681.6) |     3981.8 (3935.9) |   4584.3 (4349.2) | 3457.5 (3808.4) | 3932.8 (3989.4)
## Mean carat (SD) |       1.0 (0.5) |       0.8 (0.5) |           0.8 (0.5) |         0.9 (0.5) |       0.7 (0.4) |       0.8 (0.5)

t-Test

d %>%
  filter(cut == "Fair" | cut == "Ideal") %>%
  droplevels() %>%
  t.test(carat ~ cut, data = .) %>%
  report()

The Welch Two Sample t-test suggests that the difference of carat by cut (mean in group Fair = 1.05, mean in group Ideal = 0.70) is significant (difference = 0.34, 95% CI [0.32, 0.37], t(1781.99) = 26.00, p < .001) and can be considered as very large (Cohen’s d = 1)., The Welch Two Sample t-test suggests that the difference of carat by cut (mean in group Fair = 1.05, mean in group Ideal = 0.70) is significant (difference = 0.34, 95% CI [0.32, 0.37], t(1781.99) = 26.00, p < .001) and can be considered as very large (Cohen’s d = 1)., The Welch Two Sample t-test suggests that the difference of carat by cut (mean in group Fair = 1.05, mean in group Ideal = 0.70) is significant (difference = 0.34, 95% CI [0.32, 0.37], t(1781.99) = 26.00, p < .001) and can be considered as very large (Cohen’s d = 1). and The Welch Two Sample t-test suggests that the difference of carat by cut (mean in group Fair = 1.05, mean in group Ideal = 0.70) is significant (difference = 0.34, 95% CI [0.32, 0.37], t(1781.99) = 26.00, p < .001) and can be considered as very large (Cohen’s d = 1).

ANOVA (base)

stdaov <- aov(price ~ color * cut, data = d)
stdaov %>%
  report()

The ANOVA suggests that:

The main effect of color is significant (F(6, 53905) = 294.07, p < .001) and can be considered as small (partial omega squared = 0.03).
The main effect of cut is significant (F(4, 53905) = 159.36, p < .001) and can be considered as small (partial omega squared = 0.01).
The interaction between color and cut is significant (F(24, 53905) = 4.53, p < .001) and can be considered as very small (partial omega squared = 0.00).

ANOVA (afex)

library(afex)
d$id <- 1:length(d$carat)
afexaov <- aov_ez("id", dv = "price", between = c("color", "cut"), data = d)
afexaov$aov %>%
  report()

The ANOVA suggests that:

The main effect of color is significant (F(6, 53905) = 294.07, p < .001) and can be considered as small (partial omega squared = 0.03).
The main effect of cut is significant (F(4, 53905) = 159.36, p < .001) and can be considered as small (partial omega squared = 0.01).
The interaction between color and cut is significant (F(24, 53905) = 4.53, p < .001) and can be considered as very small (partial omega squared = 0.00).

afexaov$aov %>%
  report() %>%
  table_short()

## Parameter | Sum_Squares |    df | Mean_Square |      F |    p | Omega_Sq_partial
## --------------------------------------------------------------------------------
## color     | 2.68491e+10 |     6 | 4.47485e+09 | 294.07 | 0.00 |             0.03
## cut       | 9.69968e+09 |     4 | 2.42492e+09 | 159.36 | 0.00 |             0.01
## color:cut | 1.65346e+09 |    24 | 6.88940e+07 |   4.53 | 0.00 |             0.00
## Residuals | 8.20271e+11 | 53905 | 1.52170e+07 |        |      |

LMM

d %>%
  filter(cut == "Fair" | cut == "Ideal") %>%
  droplevels() %>%
  lmer(price ~ carat + cut + (1 | carat), data = .) %>%
  report()

We fitted a linear mixed model (estimated using REML and nloptwrap optimizer) to predict price with carat and cut (formula = price ~ carat + cut). The model included carat as random effects (formula = ~1 | carat). Standardized parameters were obtained by fitting the model on a standardized version of the dataset. Effect sizes were labelled following Funder’s (2019) recommendations.The model’s total explanatory power is substantial (conditional R2 = 0.87) and the part related to the fixed effects alone (marginal R2) is of 0.57. The model’s intercept, corresponding to price = 0, carat = 0 and cut = Fair, is at -1192.60 (SE = 273.06, 95% CI [-1727.79, -657.41], p < .001). Within this model:

The effect of carat is positive and can be considered as very large and significant (beta = 6346.99, SE = 165.26, 95% CI [6023.09, 6670.89], std. beta = 1.67, p < .001).
The effect of cut.L is positive and can be considered as small and significant (beta = 1129.24, SE = 26.68, 95% CI [1076.95, 1181.54], std. beta = 0.30, p < .001).

Daten untersuchen

Das `dlookr`-Paket

# install.packages("dlookr")
library(dlookr)

Datenblatt diagonstizieren

# check for missing data and distinct values per column
d %>%
  diagnose()

## # A tibble: 11 x 6
##    variables types   missing_count missing_percent unique_count unique_rate
##    <chr>     <chr>           <int>           <dbl>        <int>       <dbl>
##  1 carat     numeric             0               0          273   0.00506  
##  2 cut       ordered             0               0            5   0.0000927
##  3 color     ordered             0               0            7   0.000130 
##  4 clarity   ordered             0               0            8   0.000148 
##  5 depth     numeric             0               0          184   0.00341  
##  6 table     numeric             0               0          127   0.00235  
##  7 price     integer             0               0        11602   0.215    
##  8 x         numeric             0               0          554   0.0103   
##  9 y         numeric             0               0          552   0.0102   
## 10 z         numeric             0               0          375   0.00695  
## 11 id        integer             0               0        53940   1

# descriptive statistics of all numeric variables (min, max, mean, etc.)
d %>%
  diagnose_numeric()

## # A tibble: 8 x 10
##   variables   min       Q1      mean  median      Q3     max  zero minus outlier
##   <chr>     <dbl>    <dbl>     <dbl>   <dbl>   <dbl>   <dbl> <int> <int>   <int>
## 1 carat       0.2     0.4      0.798 7.00e-1  1.04e0  5.01e0     0     0    1889
## 2 depth      43      61       61.7   6.18e+1  6.25e1  7.90e1     0     0    2545
## 3 table      43      56       57.5   5.70e+1  5.90e1  9.50e1     0     0     605
## 4 price     326     950     3933.    2.40e+3  5.32e3  1.88e4     0     0    3538
## 5 x           0       4.71     5.73  5.70e+0  6.54e0  1.07e1     8     0      32
## 6 y           0       4.72     5.73  5.71e+0  6.54e0  5.89e1     7     0      29
## 7 z           0       2.91     3.54  3.53e+0  4.04e0  3.18e1    20     0      49
## 8 id          1   13486.   26970.    2.70e+4  4.05e4  5.39e4     0     0       0

# values and distribution of all categorical variables
d %>%
  diagnose_category()

## # A tibble: 20 x 6
##    variables levels        N  freq ratio  rank
##    <chr>     <ord>     <int> <int> <dbl> <int>
##  1 cut       Ideal     53940 21551 40.0      1
##  2 cut       Premium   53940 13791 25.6      2
##  3 cut       Very Good 53940 12082 22.4      3
##  4 cut       Good      53940  4906  9.10     4
##  5 cut       Fair      53940  1610  2.98     5
##  6 color     G         53940 11292 20.9      1
##  7 color     E         53940  9797 18.2      2
##  8 color     F         53940  9542 17.7      3
##  9 color     H         53940  8304 15.4      4
## 10 color     D         53940  6775 12.6      5
## 11 color     I         53940  5422 10.1      6
## 12 color     J         53940  2808  5.21     7
## 13 clarity   SI1       53940 13065 24.2      1
## 14 clarity   VS2       53940 12258 22.7      2
## 15 clarity   SI2       53940  9194 17.0      3
## 16 clarity   VS1       53940  8171 15.1      4
## 17 clarity   VVS2      53940  5066  9.39     5
## 18 clarity   VVS1      53940  3655  6.78     6
## 19 clarity   IF        53940  1790  3.32     7
## 20 clarity   I1        53940   741  1.37     8

# show outlier information for all numerical variables
d %>%
  diagnose_outlier()

##   variables outliers_cnt outliers_ratio outliers_mean   with_mean without_mean
## 1     carat         1889       3.502039        2.1537     0.79794      0.74874
## 2     depth         2545       4.718205       61.2048    61.74940     61.77637
## 3     table          605       1.121617       64.8430    57.45718     57.37340
## 4     price         3538       6.559140    14944.7764  3932.79972   3159.80711
## 5         x           32       0.059325        7.2394     5.73116      5.73026
## 6         y           29       0.053763        9.7734     5.73453      5.73235
## 7         z           49       0.090842        4.0547     3.53873      3.53826
## 8        id            0       0.000000           NaN 26970.50000  26970.50000

Normalverteilung

# shapiro-wilk test
d %>%
  select(price, carat, color, cut) %>%
  group_by(color) %>%
  normality()

## # A tibble: 14 x 5
##    variable color statistic  p_value sample
##    <chr>    <ord>     <dbl>    <dbl>  <dbl>
##  1 price    D         0.741 1.48e-66   5000
##  2 price    E         0.726 1.09e-67   5000
##  3 price    F         0.787 8.07e-63   5000
##  4 price    G         0.803 2.84e-61   5000
##  5 price    H         0.846 8.64e-57   5000
##  6 price    I         0.854 9.30e-56   5000
##  7 price    J         0.889 6.11e-41   2808
##  8 carat    D         0.873 2.94e-53   5000
##  9 carat    E         0.878 1.17e-52   5000
## 10 carat    F         0.909 1.36e-47   5000
## 11 carat    G         0.896 7.92e-50   5000
## 12 carat    H         0.926 2.31e-44   5000
## 13 carat    I         0.935 3.96e-42   5000
## 14 carat    J         0.955 1.64e-28   2808

Deskriptive Statistik

# tidy alternative for psych::describe
d %>%
  describe() %>%
  select(-starts_with("p")) # don't show percentiles

## # A tibble: 8 x 9
##   variable     n    na  mean    sd se_mean   IQR skewness kurtosis
##   <chr>    <int> <int> <dbl> <dbl>   <dbl> <dbl>    <dbl>    <dbl>
## 1 carat    53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618
## 2 depth    53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618
## 3 table    53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618
## 4 price    53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618
## 5 x        53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618
## 6 y        53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618
## 7 z        53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618
## 8 id       53940     0  5.73  1.12 0.00483  1.83    0.379   -0.618

# tidy alternative for psych::describeBy
d %>%
  group_by(cut) %>%
  describe(price, carat) %>%
  select(-starts_with("p")) # don't show percentiles

## # A tibble: 10 x 10
##    variable cut        n    na    mean      sd se_mean     IQR skewness kurtosis
##    <chr>    <ord>  <dbl> <dbl>   <dbl>   <dbl>   <dbl>   <dbl>    <dbl>    <dbl>
##  1 price    Fair    1610     0 4.36e+3 3.56e+3 8.87e+1 3155.      1.78     3.09 
##  2 price    Good    4906     0 3.93e+3 3.68e+3 5.26e+1 3883       1.72     3.05 
##  3 price    Very … 12082     0 3.98e+3 3.94e+3 3.58e+1 4461.      1.60     2.24 
##  4 price    Premi… 13791     0 4.58e+3 4.35e+3 3.70e+1 5250       1.33     1.07 
##  5 price    Ideal  21551     0 3.46e+3 3.81e+3 2.59e+1 3800.      1.84     2.98 
##  6 carat    Fair    1610     0 1.05e+0 5.16e-1 1.29e-2    0.5     1.69     5.34 
##  7 carat    Good    4906     0 8.49e-1 4.54e-1 6.48e-3    0.51    1.03     1.23 
##  8 carat    Very … 12082     0 8.06e-1 4.59e-1 4.18e-3    0.61    0.994    0.896
##  9 carat    Premi… 13791     0 8.92e-1 5.15e-1 4.39e-3    0.79    0.862    0.431
## 10 carat    Ideal  21551     0 7.03e-1 4.33e-1 2.95e-3    0.66    1.34     1.63

Komplette Diagnoseberichte (standardmäßig als PDF)

# generate pdf report for various diagnosis tasks
# d %>%
#     diagnose_report()

# generate pdf report for exploratory data analysis
# (including correlations and transform ations)
# d %>%
#     eda_report()

Bildverarbeitung (und -bearbeitung) in R

magick

https://cran.r-project.org/web/packages/magick/vignettes/intro.html

# install.packages("magick")
library(magick)

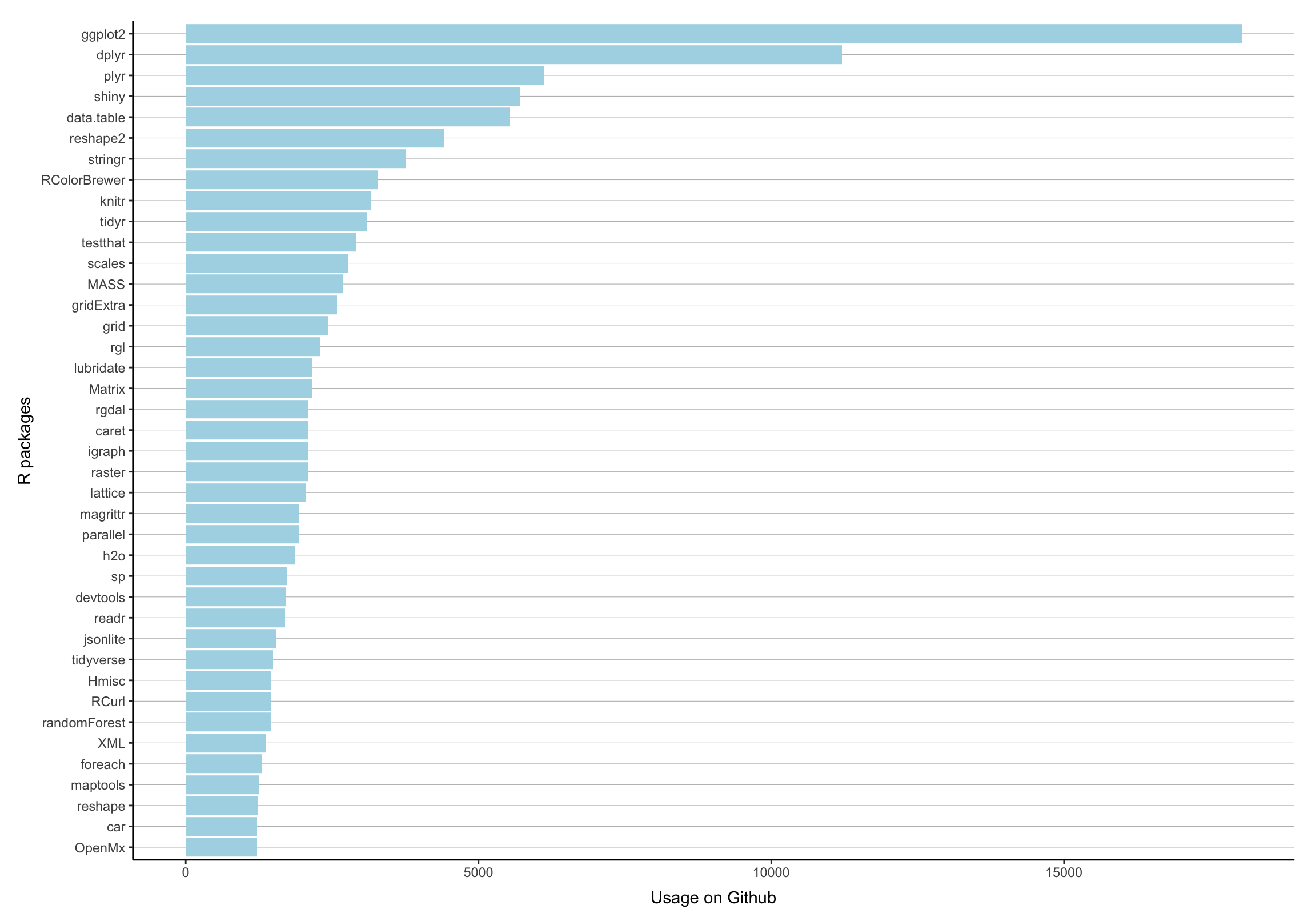
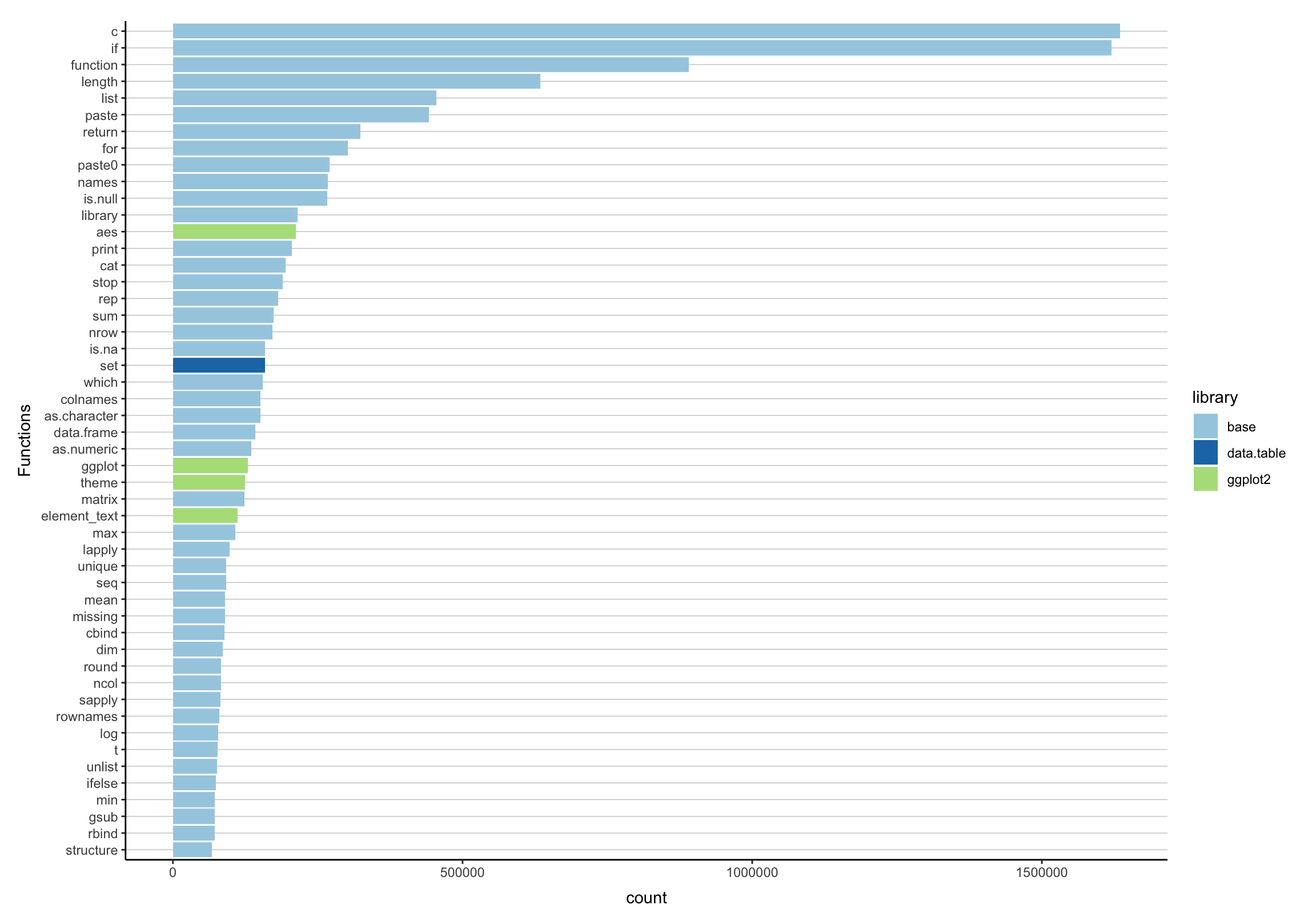
Popularity Contest

Die populärsten Pakete

Hier geklaut: https://github.com/v-kozhevnikov

Die populärsten Pakete

Hier geklaut: https://github.com/v-kozhevnikov

fin

Anhang: Die wichtigsten Funktionen

Allgemein

Hier geklaut: http://www.sr.bham.ac.uk/~ajrs/R/r-function_list.html

builtins() # List all built-in functions
options()  # Set options to control how R computes & displays results

?NA        # Help page on handling of missing data values
abs(x)     # The absolute value of "x"
append()   # Add elements to a vector
c(x)       # A generic function which combines its arguments 
cat(x)     # Prints the arguments
cbind()    # Combine vectors by row/column (cf. "paste" in Unix)
diff(x)    # Returns suitably lagged and iterated differences
gl()       # Generate factors with the pattern of their levels
grep()     # Pattern matching
identical()  # Test if 2 objects are *exactly* equal
jitter()     # Add a small amount of noise to a numeric vector
julian()     # Return Julian date
length(x)    # Return no. of elements in vector x
ls()         # List objects in current environment
mat.or.vec() # Create a matrix or vector
paste(x)     # Concatenate vectors after converting to character
range(x)     # Returns the minimum and maximum of x
rep(1,5)     # Repeat the number 1 five times
rev(x)       # List the elements of "x" in reverse order
seq(1,10,0.4)  # Generate a sequence (1 -> 10, spaced by 0.4)
sequence()     # Create a vector of sequences
sign(x)        # Returns the signs of the elements of x
sort(x)        # Sort the vector x
order(x)       # list sorted element numbers of x
tolower(),toupper()  # Convert string to lower/upper case letters
unique(x)      # Remove duplicate entries from vector
system("cmd")  # Execute "cmd" in operating system (outside of R)
vector()       # Produces a vector of given length and mode

formatC(x)     # Format x using 'C' style formatting specifications
floor(x), ceiling(x), round(x), signif(x), trunc(x)   # rounding functions

Sys.getenv(x)  # Get the value of the environment variable "x"
Sys.putenv(x)  # Set the value of the environment variable "x"
Sys.time()     # Return system time
Sys.Date()     # Return system date
getwd()        # Return working directory
setwd()        # Set working directory
?files         # Help on low-level interface to file system
list.files()   # List files in a give directory
file.info()    # Get information about files

# Built-in constants:
pi,letters,LETTERS   # Pi, lower & uppercase letters, e.g. letters[7] = "g"
month.abb,month.name # Abbreviated & full names for months

Mathe

Hier geklaut: http://www.sr.bham.ac.uk/~ajrs/R/r-function_list.html

log(x),logb(),log10(),log2(),exp(),expm1(),log1p(),sqrt()   # Fairly obvious
cos(),sin(),tan(),acos(),asin(),atan(),atan2()       # Usual stuff
cosh(),sinh(),tanh(),acosh(),asinh(),atanh()         # Hyperbolic functions
union(),intersect(),setdiff(),setequal()             # Set operations
+,-,*,/,^,%%,%/%                                     # Arithmetic operators
<,>,<=,>=,==,!=                                      # Comparison operators
eigen()      # Computes eigenvalues and eigenvectors

deriv()      # Symbolic and algorithmic derivatives of simple expressions
integrate()  # Adaptive quadrature over a finite or infinite interval.

sqrt(),sum()
?Control     # Help on control flow statements (e.g. if, for, while)
?Extract     # Help on operators acting to extract or replace subsets of vectors
?Logic       # Help on logical operators
?Mod         # Help on functions which support complex arithmetic in R
?Paren       # Help on parentheses
?regex       # Help on regular expressions used in R
?Syntax      # Help on R syntax and giving the precedence of operators
?Special     # Help on special functions related to beta and gamma functions

Statistik

Hier geklaut: http://www.sr.bham.ac.uk/~ajrs/R/r-function_list.html

help(package=stats)   # List all stats functions

?Chisquare            # Help on chi-squared distribution functions
?Poisson              # Help on Poisson distribution functions
help(package=survival) # Survival analysis

cor.test()            # Perform correlation test
cumsum(); cumprod(); cummin(); cummax()   # Cumuluative functions for vectors
density(x)            # Compute kernel density estimates
ks.test()             # Performs one or two sample Kolmogorov-Smirnov tests
loess(), lowess()     # Scatter plot smoothing
mad()                 # Calculate median absolute deviation
mean(x), weighted.mean(x), median(x), min(x), max(x), quantile(x)
rnorm(), runif()  # Generate random data with Gaussian/uniform distribution
splinefun()           # Perform spline interpolation
smooth.spline()       # Fits a cubic smoothing spline
sd()                  # Calculate standard deviation
summary(x)            # Returns a summary of x: mean, min, max etc.
t.test()              # Student's t-test
var()                 # Calculate variance
sample()              # Random samples & permutations
ecdf()                # Empirical Cumulative Distribution Function
qqplot()              # quantile-quantile plot

Extrasitzung

Einfach Textdateien speichern

Daten

sink

Funktionen aus dem tidyverse

Tidyverse

Funktionen, die man kennen sollte

Pipe %>%

Beispiele

Weitere Beispiele

Vorkommen zählen

Zählen und Sortieren

Sortieren und Spalten auswählen

Gruppieren und rechnen

Gruppieren, berechnen, filtern

Gruppenkorrelationen plotten

Filtern und plotten

Ein Tutorial

Speed-Up

For-Loops

Loops

Loops

Übung

Lösungen

Lösungen

Funktionen, die das Coden erleichtern

Daten

by()

with()

with()

with()

attach()

apply()-Familie

apply()-Familie

Unterschied by() und tapply()

Janitor-Paket

Installieren und laden

Bessere Häufigkeitstabellen

Bessere Häufigkeitstabellen

Leere Zeilen und Spalten entfernen

Spalten mit konstanten Werten entfernen

clean_names()

Automatische Tabellen mit gtsummary

Automatische Tabellen mit gtsummary

Automatische Tabellen

correlation-Paket

Automatische Berichte

report-Paket

Dataframes

t-Test

ANOVA (base)

ANOVA (afex)

LMM

Daten untersuchen

Das dlookr-Paket

Datenblatt diagonstizieren

Normalverteilung

Deskriptive Statistik

Komplette Diagnoseberichte (standardmäßig als PDF)

Bildverarbeitung (und -bearbeitung) in R

magick

Popularity Contest

Die populärsten Pakete

Die populärsten Pakete

fin

Anhang: Die wichtigsten Funktionen

Allgemein

Mathe

Statistik

`correlation`-Paket

`report`-Paket

Das `dlookr`-Paket