Sitzung 7

Wiederholung

Das Wichtigste vom letzten Mal

Pakete installieren und laden

install.packages("PAKETNAME")
library(PAKETNAME)

Deskriptive Statistik

library(psych)
describeBy(d$judgment, list(d$wordorder, d$quantifier),
  digits = 2, mat = T)

Das Wichtigste vom letzten Mal

Funktionen schreiben

my.ends <- function(vector) {
  answer <- c(vector[1], vector[length(vector)])
  answer
}

Daten transponieren

library(reshape2)
cast(id + age + gender ~ condition,
  value.var = "judgment") # long zu wide
melt(d, id.vars = c("id", "age", "gender")) # wide zu long

Fehlertypen

Fehlertypen: Erinnerungshilfe

\(\chi^2\)-Test

Daten

Übersicht zahlreicher Metriken von Studierenden an irgendeiner Hochschule.

Von der Website:

d <- read.csv("docs/data/tut7/studentsmajor.csv")
head(d, 3)

##   stud.id                name gender age height weight   religion nc.score
## 1  833917 Gonzales, Christina Female  19    160   64.8     Muslim     1.91
## 2  898539      Lozano, T'Hani Female  19    172   73.0      Other     1.56
## 3  379678      Williams, Hanh Female  22    168   70.6 Protestant     1.24
##   semester             major                      minor score1 score2
## 1      1st Political Science            Social Sciences     NA     NA
## 2      2nd   Social Sciences Mathematics and Statistics     NA     NA
## 3      3rd   Social Sciences Mathematics and Statistics     45     46
##   online.tutorial graduated salary
## 1               0         0     NA
## 2               0         0     NA
## 3               0         0     NA

Daten

Anforderungen des \(\chi^2\)-Tests:

Kategoriale Daten
Unabhängige Beobachtungen

str(d)

## 'data.frame':    8239 obs. of  16 variables:
##  $ stud.id        : int  833917 898539 379678 807564 383291 256074 754591 146494 723584 314281 ...
##  $ name           : Factor w/ 8174 levels "Aarvold, Cindi",..: 2480 4196 7858 5109 5770 5592 1258 162 7221 5240 ...
##  $ gender         : Factor w/ 2 levels "Female","Male": 1 1 1 2 1 2 1 1 2 1 ...
##  $ age            : int  19 19 22 19 21 19 21 21 18 18 ...
##  $ height         : int  160 172 168 183 175 189 156 167 195 165 ...
##  $ weight         : num  64.8 73 70.6 79.7 71.4 85.8 65.9 65.7 94.4 66 ...
##  $ religion       : Factor w/ 5 levels "Catholic","Muslim",..: 2 4 5 4 1 1 5 4 4 3 ...
##  $ nc.score       : num  1.91 1.56 1.24 1.37 1.46 1.34 1.11 2.03 1.29 1.19 ...
##  $ semester       : Factor w/ 7 levels ">6th","1st","2nd",..: 2 3 4 3 2 3 3 4 4 3 ...
##  $ major          : Factor w/ 6 levels "Biology","Economics and Finance",..: 5 6 6 3 3 5 5 5 2 3 ...
##  $ minor          : Factor w/ 6 levels "Biology","Economics and Finance",..: 6 4 4 4 4 4 6 2 3 4 ...
##  $ score1         : int  NA NA 45 NA NA NA NA 58 57 NA ...
##  $ score2         : int  NA NA 46 NA NA NA NA 62 67 NA ...
##  $ online.tutorial: int  0 0 0 0 0 0 0 0 0 0 ...
##  $ graduated      : int  0 0 0 0 0 0 0 0 0 0 ...
##  $ salary         : num  NA NA NA NA NA NA NA NA NA NA ...

Häufigkeitstabelle

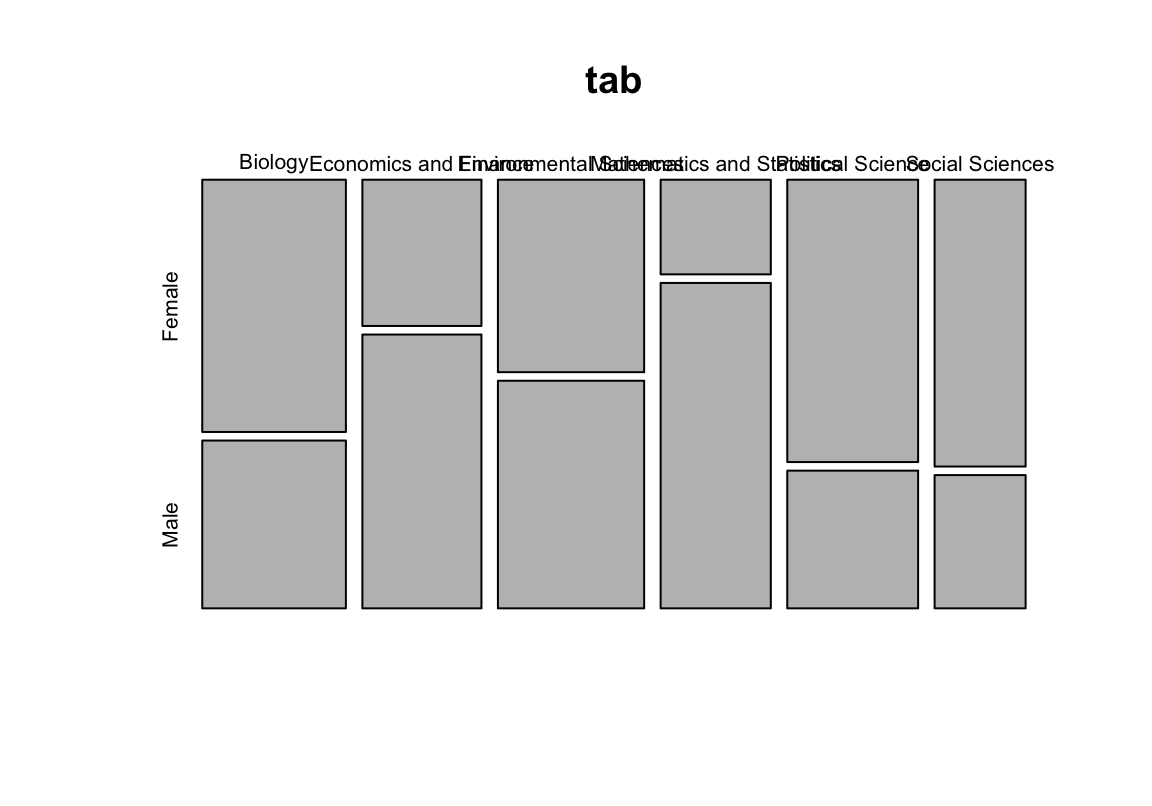
Kategoriale Variablen aufeinander abbilden

tab <- table(d$major, d$gender)
tab

##                             
##                              Female Male
##   Biology                       959  638
##   Economics and Finance         461  863
##   Environmental Sciences        745  881
##   Mathematics and Statistics    276  949
##   Political Science             978  477
##   Social Sciences               691  321

Relative Häufigkeiten

prop.table(tab, margin = 1) * 100

##                             
##                                Female     Male
##   Biology                    60.05009 39.94991
##   Economics and Finance      34.81873 65.18127
##   Environmental Sciences     45.81796 54.18204
##   Mathematics and Statistics 22.53061 77.46939
##   Political Science          67.21649 32.78351
##   Social Sciences            68.28063 31.71937

Grafische Übersicht

plot(tab)

\(\chi^2\) berechnen

options(scipen = 999)
chisq.test(d$gender, d$major)

## 
##  Pearson's Chi-squared test
## 
## data:  d$gender and d$major
## X-squared = 875.44, df = 5, p-value < 0.00000000000000022

P-Werte

Übungen

Erstellt eine Tabelle, die das Studienfach nach Religionszugehörigkeit auszählt (einmal als absolute Häufigkeiten, einmal in Prozent)
Plottet die Tabelle
Berechnet den dazugehörigen \(\chi^2\)-Test

Lösungen

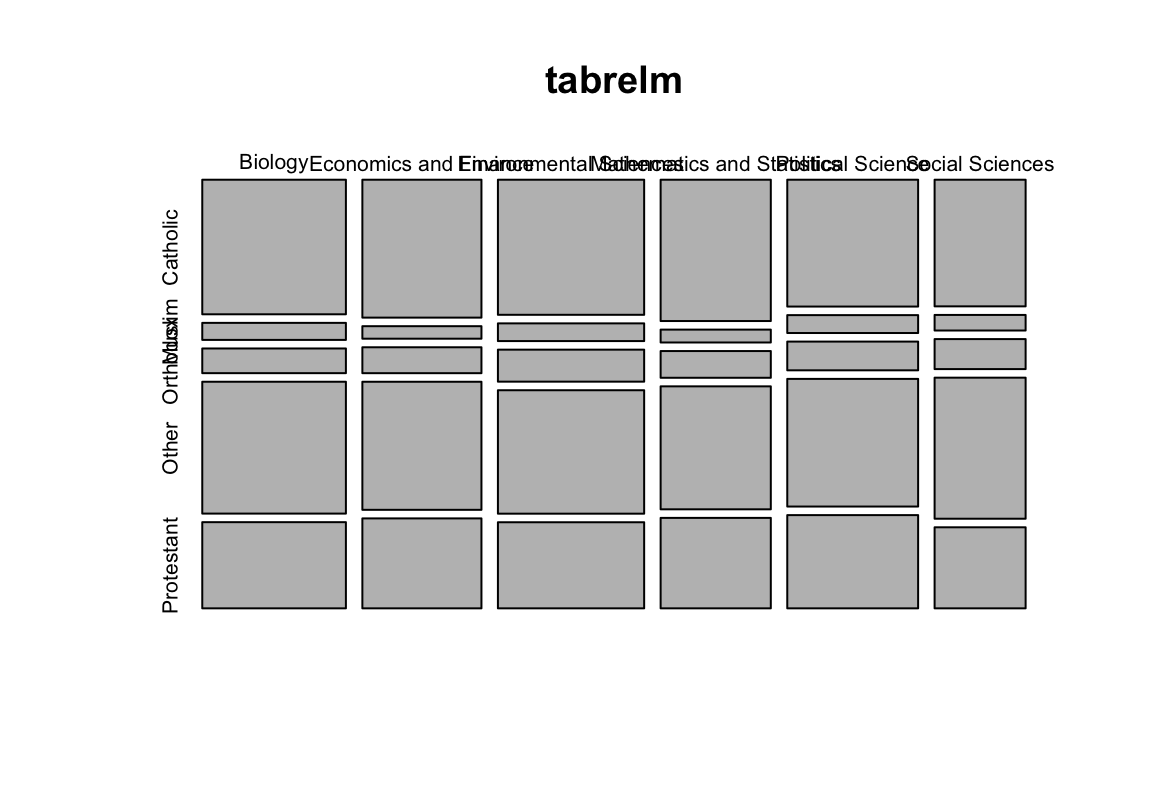
Erstellt eine Tabelle, die das Studienfach nach Religionszugehörigkeit auszählt (einmal als absolute Häufigkeiten, einmal in Prozent)

tabrelm <- table(d$major, d$religion)
prop.table(tabrelm, margin = 1) * 100

##                             
##                               Catholic    Muslim  Orthodox     Other Protestant
##   Biology                    34.126487  4.320601  6.261741 33.437696  21.853475
##   Economics and Finance      34.969789  3.172205  6.570997 32.477341  22.809668
##   Environmental Sciences     34.255843  4.489545  8.118081 31.303813  21.832718
##   Mathematics and Statistics 35.836735  3.265306  6.775510 31.183673  22.938776
##   Political Science          32.164948  4.536082  7.285223 32.371134  23.642612
##   Social Sciences            32.114625  3.952569  7.608696 35.770751  20.553360

Lösungen

Plottet die Tabelle

plot(tabrelm)

Lösungen

Berechnet den dazugehörigen \(\chi^2\)-Test

chisq.test(d$religion, d$major)

## 
##  Pearson's Chi-squared test
## 
## data:  d$religion and d$major
## X-squared = 23.881, df = 20, p-value = 0.2476

Übungen II

Erstellt ein Subset mit den drei größten Religionen
Erstellt eine Tabelle, die die Religionszugehörigkeit nach Geschlecht auszählt (einmal als absolute Häufigkeiten, einmal in Prozent)
Plottet die Tabelle
Berechnet den dazugehörigen \(\chi^2\)-Test

Lösungen II

Erstellt ein Subset mit den drei größten Religionen

dsub <- subset(d, religion %in% c("Catholic", "Other", "Protestant"))
# alternative_1: dsub <- d[d$religion %in% c(”Catholic”, ”Other”, ”Protestant”), ]
# alternative_2: dsub <- d[d$religion == “Catholic” | d$religion == “Other” | d$religion == “Protestant”, ]

# alternative: dsub$religion <- factor(dsub$religion )
dsub <- droplevels(dsub)

Zur Erinnerung: droplevels

a <- c("a", "b", "c")
a <- factor(a)
a

## [1] a b c
## Levels: a b c

a <- a[1:2]
a

## [1] a b
## Levels: a b c

a <- droplevels(a)
a

## [1] a b
## Levels: a b

Lösungen II

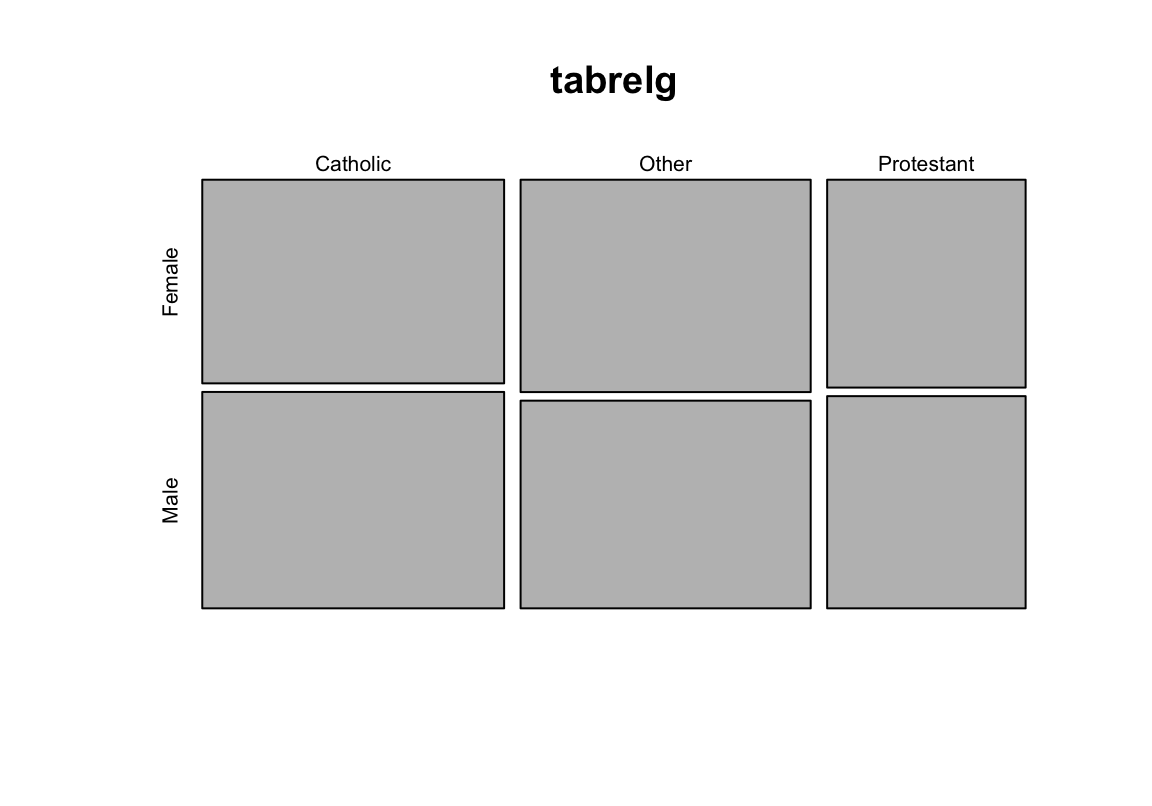
Erstellt eine Tabelle, die die Religionszugehörigkeit nach Geschlecht auszählt (einmal als absolute Häufigkeiten, einmal in Prozent)

tabrelg <- table(dsub$religion, dsub$gender)
prop.table(tabrelg, margin = 1) * 100

##             
##                Female     Male
##   Catholic   48.48051 51.51949
##   Other      50.55804 49.44196
##   Protestant 49.48341 50.51659

Lösungen II

Plottet die Tabelle

plot(tabrelg)

Lösungen II

Berechnet den dazugehörigen \(\chi^2\)-Test

chisq.test(dsub$religion, dsub$gender)

## 
##  Pearson's Chi-squared test
## 
## data:  dsub$religion and dsub$gender
## X-squared = 2.3668, df = 2, p-value = 0.3062

\(t\)-test

Zwei Arten

t.test(WerteGruppe1, WerteGruppe2, paired = TRUE / FALSE,
  var.equal = TRUE) # var.equal = F = Welch's Test

Alternative:

t.test(AV ~ Gruppenvariable, data = d, paired = TRUE / FALSE,
  var.equal = TRUE)

paired = TRUE

Abhängige Beobachtungen/Stichproben: Oft Messwiederholung: within-subjects

paired = FALSE

Unabhängige Beobachtungen/Stichproben: between-subjects
Voraussetzungen für die Anwendung des indepedent t-tests:
- Unabhängige Variable sollte aus zwei kategorialverteilten Gruppen bestehen
- Die Beobachtungen sollten unabhängig sein
- Die abhängige Variable sollte innerhalb der beiden Gruppen ungefähr normalverteilt sein
- Varianzhomogenität

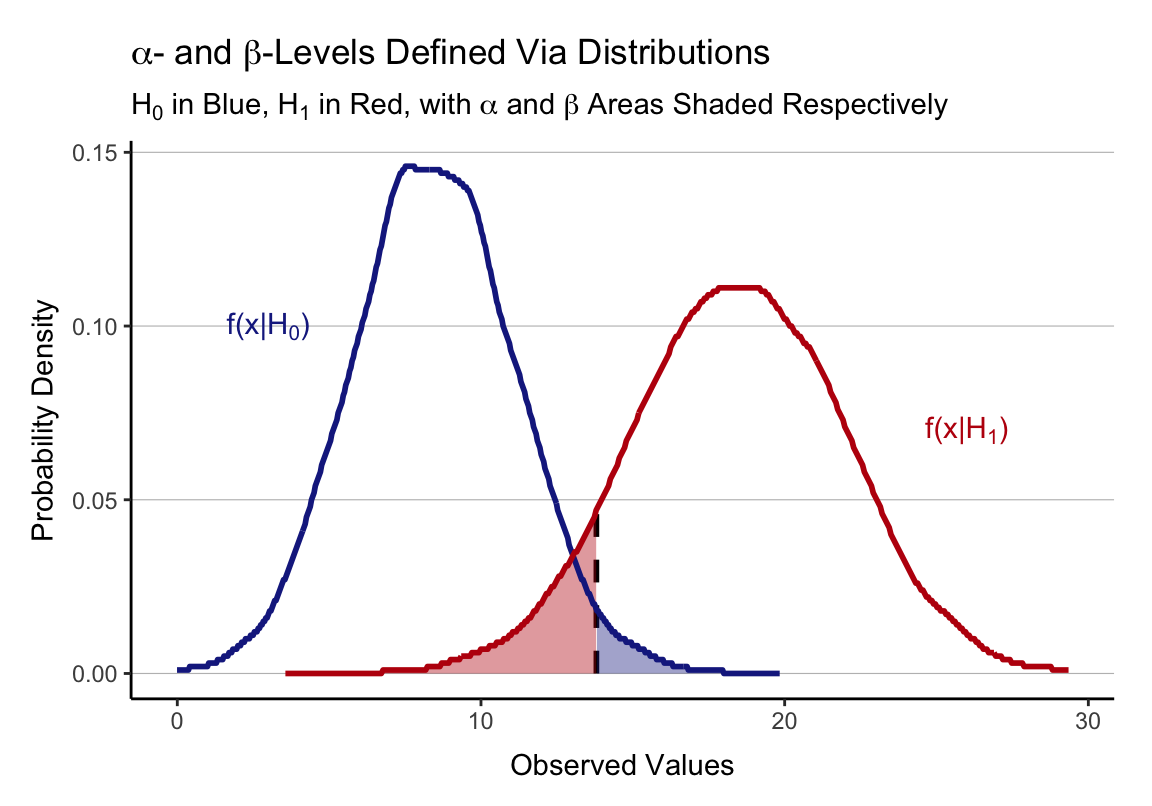
Interlude: Warum Normalverteilung?

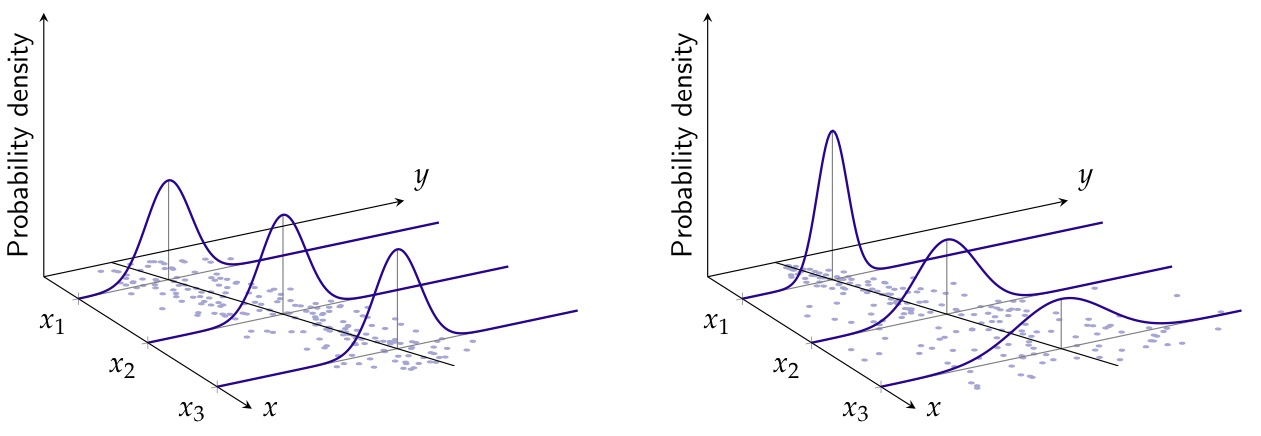
Interlude: Warum Varianzhomogenität/Homoskedastizität?

Übung III

Lese die Daten, die in “student-mat.csv” enthalten, sind in R ein. Die relevanten Spalten, die wir uns im Folgenden genauer angucken wollen, sind “sex” und “G3”. Erstelle ein entsprechendes Subset der Daten und verschaffe dir einen Überblick.
Überprüfe/Begründe, ob die folgenden Voraussetzungen gelten:

Unabhängige Variable sollte aus zwei kategorialverteilten Gruppen bestehen
Die Beobachtungen sollten unabhängig sein
Die abhängige Variable sollte innerhalb der beiden Gruppen ungefähr normalverteilt sein
Varianzhomogenität

Lösungen III

Lese die Daten, die in “student-mat.csv” enthalten, sind in R ein, erstelle ein Subset und verschaffe dir einen Überblick.

d <- read.csv("docs/data/tut7/student-mat.csv")
dsub <- subset(d, select = c("sex", "G3"))
head(dsub)

##   sex G3
## 1   F  6
## 2   F  6
## 3   F 10
## 4   F 15
## 5   F 10
## 6   M 15

summary(dsub)

##  sex           G3       
##  F:208   Min.   : 0.00  
##  M:187   1st Qu.: 8.00  
##          Median :11.00  
##          Mean   :10.42  
##          3rd Qu.:14.00  
##          Max.   :20.00

Lösungen III

Überprüfe/Begründe, ob die folgenden Voraussetzungen gelten:

Unabhängige Variable sollte aus zwei kategorialverteilten Gruppen bestehen

length(levels(dsub$sex)) == 2

## [1] TRUE

Die Beobachtungen sollten unabhängig sein

Sex, so nehmen wir zumindest für die Zwecke dieser Übung an, ist binär- und disjunktverteilt. Die Anforderung ist also erfüllt, weil kein Schüler sowohl der Männer- als auch der Frauengruppe angehört.

Lösungen III

Die abhängige Variable sollte innerhalb der beiden Gruppen ungefähr normalverteilt sein

Histogramm

hist(dsub$G3, breaks = 20)

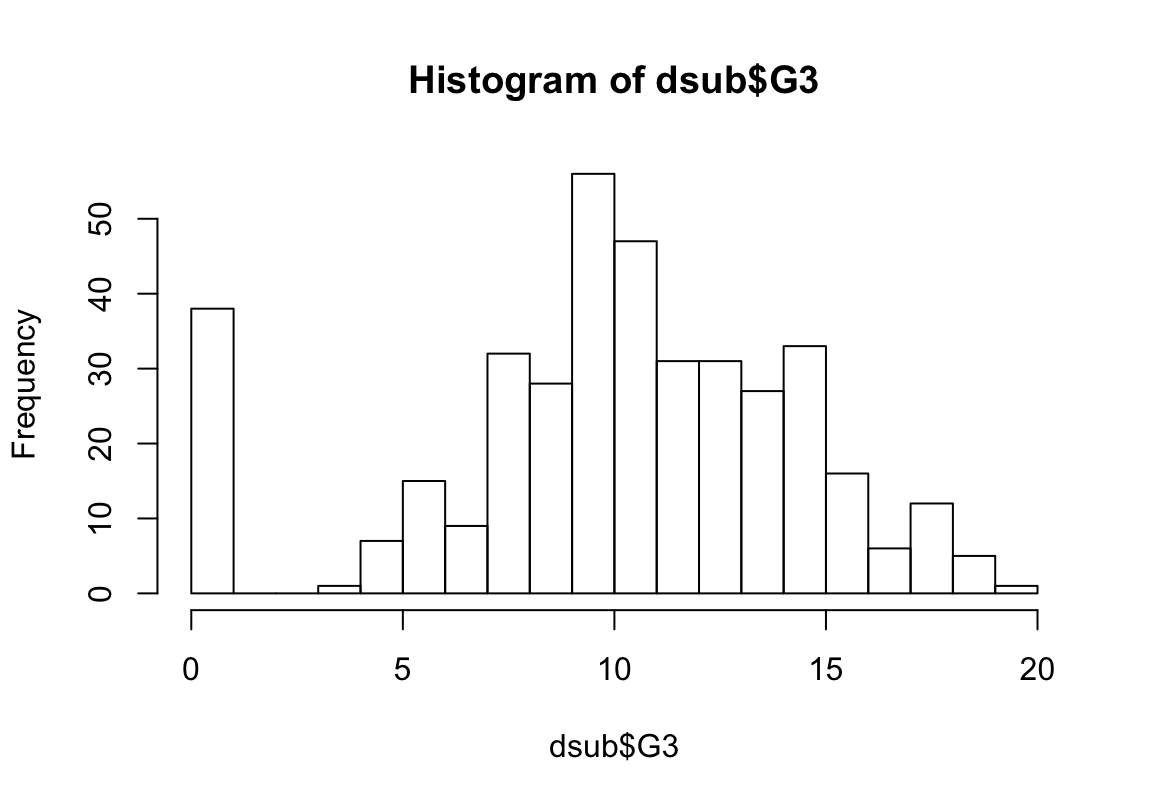
Lösungen III

zu viele 0-Ergebnisse. Die sollten wir rausnehmen

dsub <- dsub[dsub$G3 != 0, ]
hist(dsub$G3, breaks = 20)

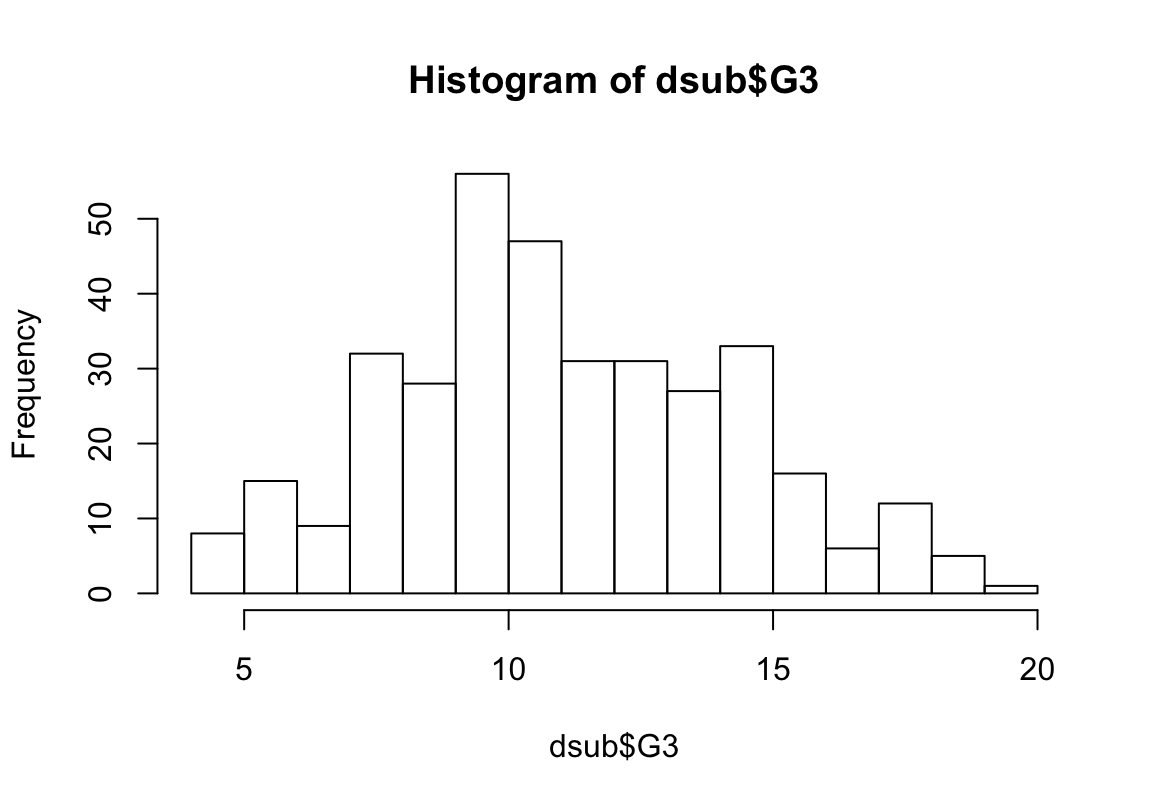
Lösungen III

Varianzhomogenität

install.packages("car")

library(car)
leveneTest(G3 ~ sex, data = dsub)

## Levene's Test for Homogeneity of Variance (center = median)
##        Df F value Pr(>F)
## group   1  0.6145 0.4336
##       355

Übung IV

Berechnet den \(t\)-test

Lösung IV

Berechnet den \(t\)-test

t.test(dsub$G3[dsub$sex == "F"], dsub$G3[dsub$sex == "M"],
  paired = F, var.equal = TRUE)

Alternative Syntax:

t.test(G3 ~ sex, data = dsub, paired = F, var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  G3 by sex
## t = -1.9405, df = 355, p-value = 0.05311
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.330667531  0.008920202
## sample estimates:
## mean in group F mean in group M 
##        11.20541        11.86628

Übung V

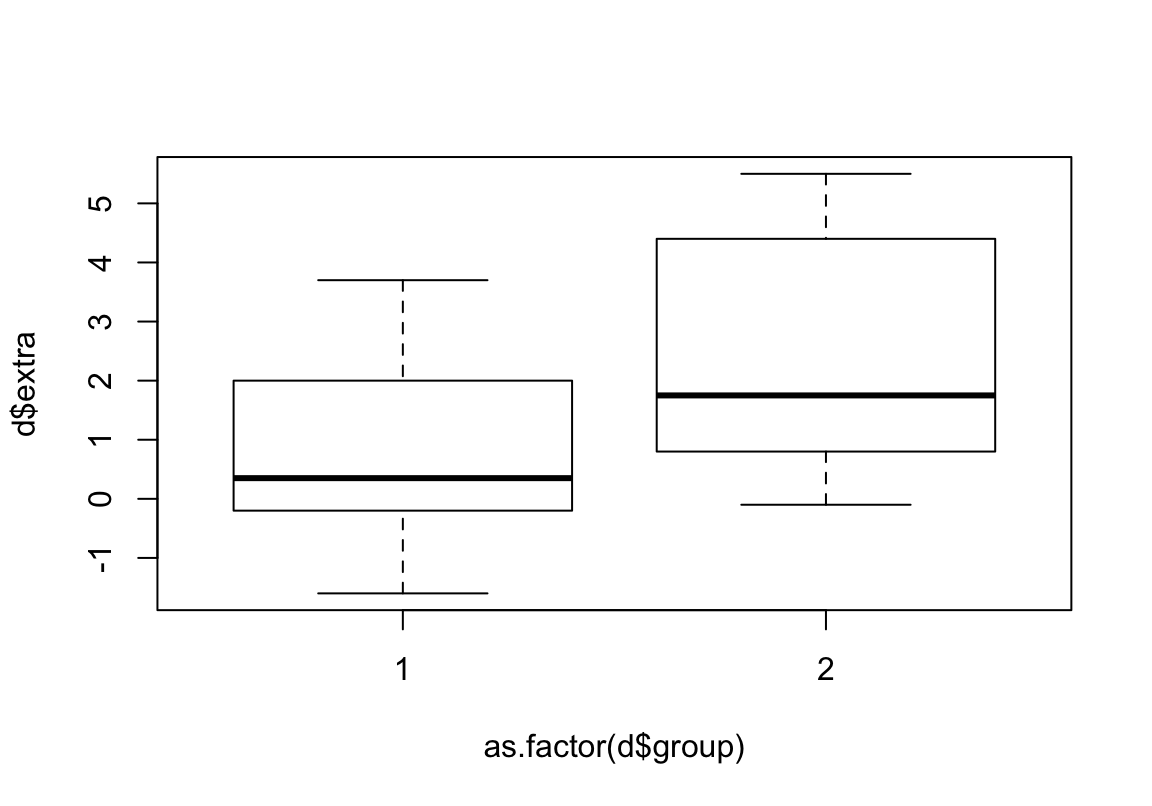
Lest die Datei “sleep.txt” ein und verschafft euch einen Überblick. Es geht hierbei um Folgendes: “Data which show the effect of two soporific drugs (increase in hours of sleep compared to control) on 10 patients.”
Berechnet den entsprechenden \(t\)-Test

Lösungen V

Lest die Datei “sleep.txt” ein und verschafft euch einen Überblick.

d <- read.table("docs/data/tut7/sleep.txt", sep = "|", header = T)
head(d)

##   extra group ID
## 1   0.7     1  1
## 2  -1.6     1  2
## 3  -0.2     1  3
## 4  -1.2     1  4
## 5  -0.1     1  5
## 6   3.4     1  6

str(d)

## 'data.frame':    20 obs. of  3 variables:
##  $ extra: num  0.7 -1.6 -0.2 -1.2 -0.1 3.4 3.7 0.8 0 2 ...
##  $ group: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ ID   : int  1 2 3 4 5 6 7 8 9 10 ...

Lösungen V

Berechnet den entsprechenden \(t\)-Test

t.test(d$extra[d$group == "1"], d$extra[d$group == "2"],
  paired = T, var.equal = TRUE)

t.test(extra ~ group, data = d, paired = T, var.equal = TRUE)

## 
##  Paired t-test
## 
## data:  extra by group
## t = -4.0621, df = 9, p-value = 0.002833
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -2.4598858 -0.7001142
## sample estimates:
## mean of the differences 
##                   -1.58

Lösungen V

Berechnet den entsprechenden \(t\)-Test

Hier habe ich die Alternativhypothese explizit angegeben. Erinnert ihr euch noch daran, was Thomas euch dazu erzählt hat?

t.test(d$extra[d$group == "1"], d$extra[d$group == "2"],
  paired = T, alternative = "less", var.equal = TRUE)

## 
##  Paired t-test
## 
## data:  d$extra[d$group == "1"] and d$extra[d$group == "2"]
## t = -4.0621, df = 9, p-value = 0.001416
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##        -Inf -0.8669947
## sample estimates:
## mean of the differences 
##                   -1.58

alternative = less

boxplot(d$extra ~ as.factor(d$group))

Übungen VI

Lest die Datei “grammar.dat” ein und verschafft euch einen Überblick. Es handelt sich hierbei um (ausdachte) Daten eines (ebenfalls ausgedachten) Experiments, in dem 10 Studierende zweimal an einem Grammatiktest teilgenommen haben. Einmal ohne Training und einmal, zu einem späteren Zeitpunkt, mit vorangestelltem Grammatikunterricht.
Wie müsste der \(t\)-Test aussehen, der die Ergebnisse dieses Experiments inferenzstatistisch überprüfen soll?

Lösungen VI

Lest die Datei “grammar.dat” ein und verschafft euch einen Überblick.

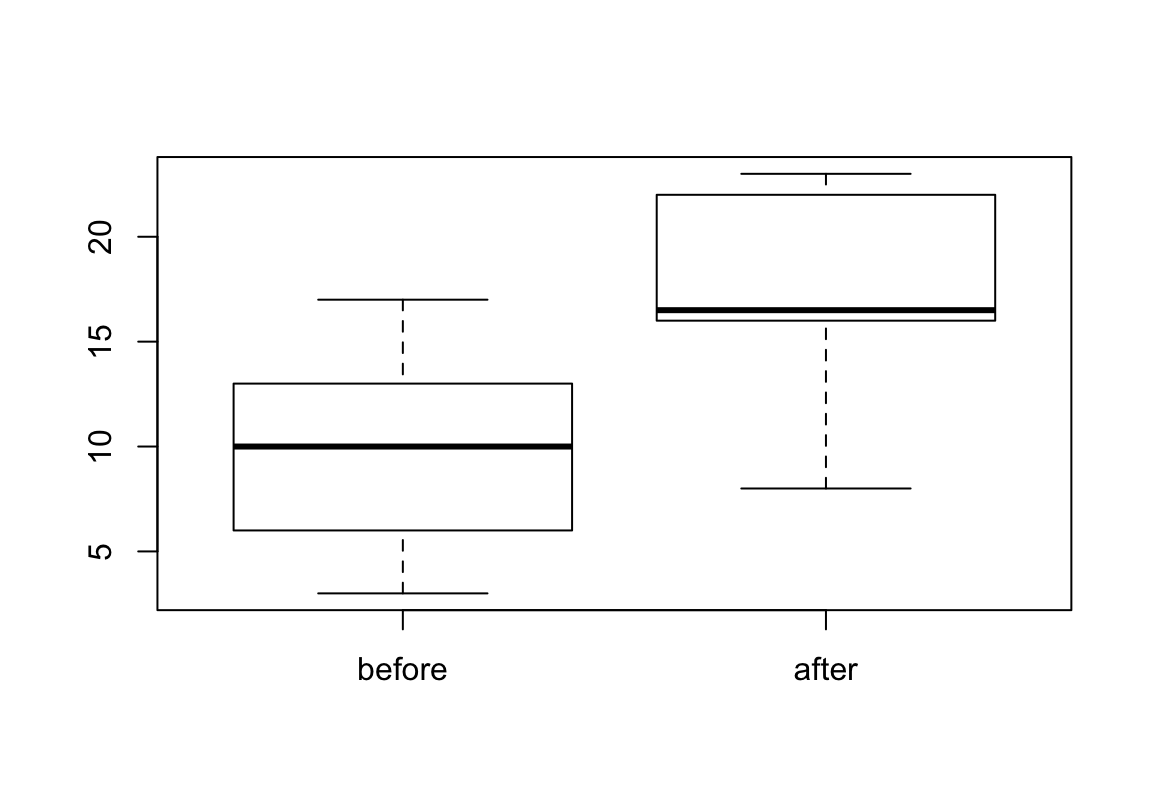
d <- read.table("docs/data/tut7/grammar.dat", sep = ";", header = T)
boxplot(d[, 1:2])

Lösungen VI

Wie müsste der \(t\)-Test aussehen, der die Ergebnisse dieses Experiments inferenzstatistisch überprüfen soll?

t.test(d$before, d$after, alternative = "less",
  paired = T, var.equal = TRUE)

## 
##  Paired t-test
## 
## data:  d$before and d$after
## t = -4.4853, df = 9, p-value = 0.0007604
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##       -Inf -4.493909
## sample estimates:
## mean of the differences 
##                    -7.6

Nur Kurz: Plots

Ein Plot zum Abschluss

library(ggplot2)
library(reshape2)

dlong <- melt(d, id.vars = "id")
dlong$id <- factor(dlong$id)
p <- ggplot(dlong, aes(y = value, x = variable, group = id)) +
  geom_line() + geom_point() +
  stat_summary(fun.y = mean, geom = "line", color = "red",
    linetype = "dashed",
    mapping = aes(x = variable, y = value, group = 1)) +
  stat_summary(fun.y = mean, geom = "point", color = "red",
    shape = 18, size = 3,
    mapping = aes(x = variable, y = value, group = 1)) +
  labs(y = "Scores", x = "Test") + cleanup

Ein Plot zum Abschluss

# mittelwert in rot und gestrichelt
p

F*ck die Uni

Schönes Wochenende!