Sitzung 8

Wiederholung

Das Wichtigste vom letzten Mal

\(\chi^2\)-Test

chisq.test(x, y)

t-Test

t.test(x, y, paired = FALSE, var.equal = T, data = d)
t.test(x, y, paired = TRUE, var.equal = T, data = d)
t.test(x, y, paired = TRUE, var.equal = T,
  alternative = "less", data = d) # "greater", "two.sided"

Alternative Syntax (lineares Modell):

t.test(AV ~ Gruppe, paired = FALSE / TRUE, var.equal = T, data = d)

Base R: ANOVA

Meme My Stats

Einleitendes

Die Varianzanalyse in R kann auf viele verschiedene Arten durchgeführt werden. Einige davon sind in base R enthalten, andere (idR komfortablere) werden durch externe Pakete zur Verfügung gestellt.

Ich zeige euch heute drei verschiedene davon:

aov()
aov_ez()
ezAnova()

Interlude: between und within

Beantwortet die unteren Fragen und gebt jeweils Beispiele (egal ob linguistischer Art oder nicht)

  1. Was bedeutet es, wenn ein Faktor within-subjects ist?
  2. Was ist mit between-subjects?
  3. Wie steht’s mit within-items?
  4. Und mit between-items?

Interlude: between und within

Beantwortet die unteren Fragen und gebt jeweils Beispiele (egal ob linguistischer Art oder nicht)

  1. Was bedeutet es, wenn ein Faktor within-subjects ist?
  • Messung von Gedächtnisleistung: Jede Person einmal ausgeruht und einmal (an einem anderen Termin) nach einer durchzechten Nacht (außerdem Messwiederholung)
  1. Was ist mit between-subjects?
  • Geschlecht; Placebo vs richtiges Medikament
  1. Wie steht’s mit within-items?
  • Item immer in zwei Ausführungen: Einmal mit Scrambling, einmal ohne
  1. Und mit between-items?
  • Itemset ist geteilt in Äußerungen mit Implikatur und Äußerungen ohne

aov()

Between-Design

summary(aov(AV ~ UVbetween, d))

Within-Design

summary(aov(AV ~ UVwithin + Error(ID - Variable / UVwithin), d))

Faktorinteraktion mit "*"

summary(aov(AV ~ UV1 * UV2, d))

Messwiederholung (within-Design)

summary(aov(AV ~ UV + Error(ID - Variable / UVwithin), d))

Messwiederholung (between-Design)

summary(aov(AV ~ UV + Error(ID - Variable), d))

aov()

Mixed-Design mit Messwiederholung

summary(aov(AV ~ UVwithin * UVbetween + Error(ID - Variable / UVwithin),
  d))

Mixed-Design mit Messwiederholung und Interaktion

summary(aov(AV ~ UVwithin1 * UVwithin2 * UVbetween +
  Error(ID - Variable / UVwithin1 * UVwithin2), d))

Übungen II

  1. Stellt euch vor, ihr werdet beauftragt folgende Volksweisheit zu testen: “Bier auf Wein, das lass sein”. Was wäre ein geeignetes Experimentdesign und wie müsste die entprechende ANOVA aussehen?

  2. Das erste Experiment liefert keine richtigen Ergebnisse. Euch kommt aber in den Sinn, dass der Spruch vielleicht von einem Mann stammt und der Rat daher vielleicht nur auf Männer zutrifft. Wie würdet ihr das testen und wie würde eine dazugehörige ANOVA aussehen?

Lösungen II

  1. Stellt euch vor, ihr werdet beauftragt folgende Volksweisheit zu testen: “Bier auf Wein, das lass sein”. Was wäre ein geeignetes Experimentdesign und wie müsste die entprechende ANOVA aussehen?
aov(AV ~ Reihenfolge + Error(ID - Variable / Reihenfolge),
  d)
  1. Das erste Experiment liefert keine richtigen Ergebnisse. Euch kommt aber in den Sinn, dass der Spruch vielleicht von einem Mann stammt und der Rat daher vielleicht nur auf Männer zutrifft. Wie würdet ihr das testen und wie würde eine dazugehörige ANOVA aussehen?
aov(AV ~ Reihenfolge * Geschlecht + Error(ID - Variable / Reihenfolge),
  d)

Übungen III

    1. Lest die Datei „LungCapData.csv“ in R ein und verschafft euch einen Überblick über die Daten.
    2. Gibt es NAs?
  2. Berechnet, ob der Faktor einen signifikaten Einfluss auf die Lungenkapazität hat.
  3. Berechnet,ob der Faktor einen signifikaten Einfluss auf die Lungenkapazität hat.
  4. Berechnet, ob es eine Interaktion zwischen den Faktoren , für die über 18-Jährigen gibt.
  5. Berechnet, ob es eine Interaktion zwischen den Faktoren , und für die über 18-Jährigen gibt.

Lösungen III

    1. Lest die Datei „LungCapData.csv“ in R ein und verschafft euch einen Überblick über die Daten.
d <- read.csv("docs/data/tut8/LungCapData.csv", sep = ";")
head(d)
##   LungCap Age Height Smoke Gender Caesarean
## 1   6.475   6   62.1    no   male        no
## 2  10.125  18   74.7   yes female        no
## 3   9.550  16   69.7    no female       yes
## 4  11.125  14   71.0    no   male        no
## 5   4.800   5   56.9    no   male        no
## 6   6.225  11   58.7    no female        no
summary(d)
##     LungCap            Age            Height      Smoke        Gender   
##  Min.   : 0.507   Min.   : 3.00   Min.   :45.30   no :648   female:358  
##  1st Qu.: 6.150   1st Qu.: 9.00   1st Qu.:59.90   yes: 77   male  :367  
##  Median : 8.000   Median :13.00   Median :65.40                         
##  Mean   : 7.863   Mean   :12.33   Mean   :64.84                         
##  3rd Qu.: 9.800   3rd Qu.:15.00   3rd Qu.:70.30                         
##  Max.   :14.675   Max.   :19.00   Max.   :81.80                         
##  Caesarean
##  no :561  
##  yes:164  
##           
##           
##           
##

Lösungen III

    1. Gibt es NAs?
# prozent NAs pro spalte
(apply(is.na(d), 2, sum) / length(d[, 1])) * 100
##   LungCap       Age    Height     Smoke    Gender Caesarean 
##         0         0         0         0         0         0
# alle zeilen mit NAs
d[!complete.cases(d), ]
## [1] LungCap   Age       Height    Smoke     Gender    Caesarean
## <0 rows> (or 0-length row.names)

Lösungen III

  1. Berechnet, ob der Faktor einen signifikaten Einfluss auf die Lungenkapazität hat.
summary(aov(LungCap ~ Gender, d))
##              Df Sum Sq Mean Sq F value     Pr(>F)    
## Gender        1    148  147.96   21.47 0.00000426 ***
## Residuals   723   4983    6.89                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
  1. Berechnet,ob der Faktor einen signifikaten Einfluss auf die Lungenkapazität hat.
summary(aov(LungCap ~ Caesarean, d))
##              Df Sum Sq Mean Sq F value Pr(>F)
## Caesarean     1      2   2.331   0.329  0.567
## Residuals   723   5128   7.093

Lösungen III

  1. Berechnet, ob es eine Interaktion zwischen den Faktoren , für die über 18-Jährigen gibt.
dsub <- subset(d, Age >= 18)
summary(aov(LungCap ~ Caesarean * Smoke, dsub))
##                 Df Sum Sq Mean Sq F value Pr(>F)
## Caesarean        1   0.01   0.010   0.005  0.947
## Smoke            1   3.77   3.768   1.638  0.205
## Caesarean:Smoke  1   1.84   1.845   0.802  0.373
## Residuals       76 174.83   2.300
  1. Berechnet, ob es eine Interaktion zwischen den Faktoren , und für die über 18-Jährigen gibt.
summary(aov(LungCap ~ Caesarean * Smoke * Gender, dsub))
##                        Df Sum Sq Mean Sq F value   Pr(>F)    
## Caesarean               1   0.01    0.01   0.005 0.941257    
## Smoke                   1   3.77    3.77   1.981 0.163565    
## Gender                  1  31.78   31.78  16.710 0.000112 ***
## Caesarean:Smoke         1   1.98    1.98   1.039 0.311355    
## Caesarean:Gender        1   2.73    2.73   1.437 0.234571    
## Smoke:Gender            1   3.04    3.04   1.598 0.210287    
## Caesarean:Smoke:Gender  1   0.23    0.23   0.120 0.730253    
## Residuals              72 136.92    1.90                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Alternative ANOVA-Befehle

afex-ANOVA

Zur Erinnerung: Die Reihenfolge der positionalen Argumente könnt ihr nur dann ignorieren, wenn ihr sie benennt. Wenn ihr sie nicht benennt, müsst ihr die untere Abfolge einhalten. Allerdings ist euer Code besser nachvollziehbar (für Kollegen, Reviewer, etc.), wenn ihr alle Argumente per Schlüsselwort angegebt (und nicht bloß positional vorgeht).

install.packages("afex")
library(afex)
aov_ez(id = "ID-Variable",
  dv = "Abhängige Variable",
  data = d,
  within = c("UVwithin1", "UVwithin2"),
  between = c("UVbetween1", "UVbetween2")
)

ez-ANOVA

install.packages("ez")
library(ez)
ezANOVA(data = d,
  dv = Abhängige - Variable,
  wid = ID - Variable,
  within = .(UVwithin1, UVwithin2),
  between = .(UVbetween1, UVbetween2))

Übungen IV

Jetzt beschäftigen wir uns mit einem Experiment, das im psycholinguistischen Experimentalpraktikum entstanden ist. Das Design ist wie folgt:

*: 24 Items, 32 Proband*innen; jede*r Proband*in sah ein Item genau einmal unter einer Bedingung, und alle Bedingungen gleich oft. Zuordnung nach lateinischem Quadrat.

    1. Der Klempner wurde ins Gefängnis begleitet, weil er seine Mutter erschlagen hatte.
    2. Der Klempner wurde ins Gefängnis begleitet, weil ein Abwasserrohr geplatzt war.
    3. Der Klempner wurde zum Gefängnis begleitet, weil er seine Mutter erschlagen hatte.
    4. Der Klempner wurde zum Gefängnis begleitet, weil ein Abwasserrohr geplatzt war.

Lest die Datei “dzi.dat” ein, verschafft euch einen Überblick und berechnet die deskriptive Statistik und die richtige ANOVA in drei Ausführungen: base R, afex und ez.

Lösungen IV

Datei einlesen

d <- read.table("docs/data/tut8/psych.dat", sep = "\t", header = T)

Überblick verschaffen

head(d)
##   gender age               fach subject variant experiment item condition
## 1      m  19 LADe-EngPhilologie       1       1          1    6         b
## 2      m  19 LADe-EngPhilologie       1       1          1   14         b
## 3      m  19 LADe-EngPhilologie       1       1          1   13         a
## 4      m  19 LADe-EngPhilologie       1       1          1   12         d
## 5      m  19 LADe-EngPhilologie       1       1          1   15         b
## 6      m  19 LADe-EngPhilologie       1       1          1    7         c
##   judgement    verb      gen prep
## 1         7 passive episodic  ins
## 2         7 passive episodic  ins
## 3         7 passive  generic  ins
## 4         7   modal episodic  zum
## 5         7 passive episodic  ins
## 6         7   modal  generic  zum

Lösungen IV

summary(d)
##  gender       age                   fach        subject        variant    
##  m:168   Min.   :18.0   De-Gesch      :114   Min.   : 1.0   Min.   :1.00  
##  w:426   1st Qu.:19.0   WiPaed        : 95   1st Qu.: 8.0   1st Qu.:2.00  
##          Median :20.0   LADe-Sport    : 54   Median :16.0   Median :4.00  
##          Mean   :21.4   De            : 38   Mean   :16.4   Mean   :4.47  
##          3rd Qu.:21.0   LADe-Gesch    : 27   3rd Qu.:25.0   3rd Qu.:7.00  
##          Max.   :33.0   De-AllgSprachw: 19   Max.   :32.0   Max.   :8.00  
##                         (Other)       :247                                
##    experiment      item       condition   judgement          verb    
##  Min.   :1    Min.   : 1.00   a:148     Min.   :1.000   modal  :314  
##  1st Qu.:1    1st Qu.: 5.00   b:150     1st Qu.:5.000   passive:280  
##  Median :1    Median :12.00   c:146     Median :7.000                
##  Mean   :1    Mean   :11.54   d:150     Mean   :5.944                
##  3rd Qu.:1    3rd Qu.:18.00             3rd Qu.:7.000                
##  Max.   :1    Max.   :23.00             Max.   :7.000                
##                                                                      
##        gen       prep    
##  episodic:300   ins:298  
##  generic :294   zum:296  
##                          
##                          
##                          
##                          
##

Lösungen IV

d[!complete.cases(d), ]
##  [1] gender     age        fach       subject    variant    experiment
##  [7] item       condition  judgement  verb       gen        prep      
## <0 rows> (or 0-length row.names)
str(d)
## 'data.frame':    594 obs. of  12 variables:
##  $ gender    : Factor w/ 2 levels "m","w": 1 1 1 1 1 1 1 1 1 1 ...
##  $ age       : int  19 19 19 19 19 19 19 19 19 19 ...
##  $ fach      : Factor w/ 19 levels "De","De-AllgSprachw",..: 11 11 11 11 11 11 11 11 11 11 ...
##  $ subject   : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ variant   : int  1 1 1 1 1 1 1 1 1 1 ...
##  $ experiment: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ item      : int  6 14 13 12 15 7 22 11 16 4 ...
##  $ condition : Factor w/ 4 levels "a","b","c","d": 2 2 1 4 2 3 3 3 3 4 ...
##  $ judgement : int  7 7 7 7 7 7 7 7 7 7 ...
##  $ verb      : Factor w/ 2 levels "modal","passive": 2 2 2 1 2 1 2 1 2 1 ...
##  $ gen       : Factor w/ 2 levels "episodic","generic": 1 1 2 1 1 2 2 2 2 1 ...
##  $ prep      : Factor w/ 2 levels "ins","zum": 1 1 1 2 1 2 2 2 2 2 ...

Faktoren erstellen

d$subject <- factor(d$subject)
d$item <- factor(d$item)

Lösungen IV

Deskriptive Statistik

library(psych)
describeBy(d$judgement, list(d$gen, d$prep), mat = T, digits = 2)
##     item   group1 group2 vars   n mean   sd median trimmed  mad min max range
## X11    1 episodic    ins    1 150 5.55 1.85      6    5.87 1.48   1   7     6
## X12    2  generic    ins    1 148 6.11 1.26      7    6.35 0.00   2   7     5
## X13    3 episodic    zum    1 150 6.08 1.34      7    6.35 0.00   1   7     6
## X14    4  generic    zum    1 146 6.04 1.39      7    6.32 0.00   1   7     6
##      skew kurtosis   se
## X11 -1.11    -0.03 0.15
## X12 -1.42     1.07 0.10
## X13 -1.61     2.20 0.11
## X14 -1.53     1.64 0.11

Lösungen IV

Base R

aovsub <- summary(aov(judgement ~ prep * gen +
  Error(subject / (prep * gen)), d))
aovitem <- summary(aov(judgement ~ (prep * gen) +
  Error(item / (prep * gen)), d))

Lösungen IV

Base R

aovsub
## 
## Error: subject
##           Df Sum Sq Mean Sq F value Pr(>F)
## prep       1    5.4   5.428   0.412  0.526
## gen        1   12.8  12.754   0.967  0.334
## prep:gen   1    2.7   2.707   0.205  0.654
## Residuals 28  369.2  13.187               
## 
## Error: subject:prep
##           Df Sum Sq Mean Sq F value Pr(>F)  
## prep       1   6.79   6.795   3.630 0.0667 .
## gen        1   0.30   0.302   0.161 0.6908  
## prep:gen   1   0.00   0.002   0.001 0.9758  
## Residuals 29  54.29   1.872                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: subject:gen
##           Df Sum Sq Mean Sq F value  Pr(>F)   
## gen        1  11.56  11.555   8.426 0.00687 **
## prep:gen   1  12.72  12.715   9.272 0.00481 **
## Residuals 30  41.14   1.371                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: subject:prep:gen
##           Df Sum Sq Mean Sq F value Pr(>F)  
## prep:gen   1  10.93  10.929   4.563 0.0407 *
## Residuals 31  74.24   2.395                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: Within
##            Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 466  721.1   1.547
aovitem
## 
## Error: item
##           Df Sum Sq Mean Sq F value Pr(>F)  
## prep       1   2.55   2.554   0.638 0.4369  
## gen        1   5.47   5.471   1.367 0.2607  
## prep:gen   1  22.72  22.718   5.674 0.0309 *
## Residuals 15  60.06   4.004                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: item:prep
##           Df Sum Sq Mean Sq F value Pr(>F)  
## prep       1   7.77   7.767   3.603 0.0759 .
## gen        1  10.85  10.854   5.035 0.0393 *
## prep:gen   1   1.99   1.986   0.921 0.3514  
## Residuals 16  34.49   2.156                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: item:gen
##           Df Sum Sq Mean Sq F value Pr(>F)
## gen        1  10.33  10.329   2.462  0.135
## prep:gen   1   0.87   0.872   0.208  0.654
## Residuals 17  71.32   4.195               
## 
## Error: item:prep:gen
##           Df Sum Sq Mean Sq F value  Pr(>F)   
## prep:gen   1  13.12  13.118   8.933 0.00787 **
## Residuals 18  26.43   1.468                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Error: Within
##            Df Sum Sq Mean Sq F value Pr(>F)
## Residuals 518   1055   2.037

Lösungen IV

afex

library(afex)
aov_ez(id = "subject", dv = "judgement", within = c("gen", "prep"),
  data = d)
## Anova Table (Type 3 tests)
## 
## Response: judgement
##     Effect    df  MSE       F  ges p.value
## 1      gen 1, 31 0.30 9.07 ** .022    .005
## 2     prep 1, 31 0.37  4.64 * .014    .039
## 3 gen:prep 1, 31 0.52  4.85 * .020    .035
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1
aov_ez(id = "item", dv = "judgement", within = c("gen", "prep"),
  data = d)
## Anova Table (Type 3 tests)
## 
## Response: judgement
##     Effect    df  MSE       F  ges p.value
## 1      gen 1, 18 0.52    2.57 .042    .126
## 2     prep 1, 18 0.34    2.69 .029    .118
## 3 gen:prep 1, 18 0.19 9.09 ** .054    .007
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '+' 0.1 ' ' 1

Lösungen IV

ez

library(ez)
ezANOVA(data = d, wid = subject, dv = judgement, within = .(prep, gen))
## $ANOVA
##     Effect DFn DFd        F           p p<.05        ges
## 2     prep   1  31 4.641385 0.039094646     * 0.01370960
## 3      gen   1  31 9.073004 0.005128325     * 0.02213167
## 4 prep:gen   1  31 4.852868 0.035162122     * 0.02039948
ezANOVA(data = d, wid = item, dv = judgement, within = .(prep, gen))
## $ANOVA
##     Effect DFn DFd        F           p p<.05        ges
## 2     prep   1  18 2.694220 0.118069072       0.02947056
## 3      gen   1  18 2.574507 0.125999408       0.04226753
## 4 prep:gen   1  18 9.087690 0.007445464     * 0.05379394

Nur Kurz: Plots

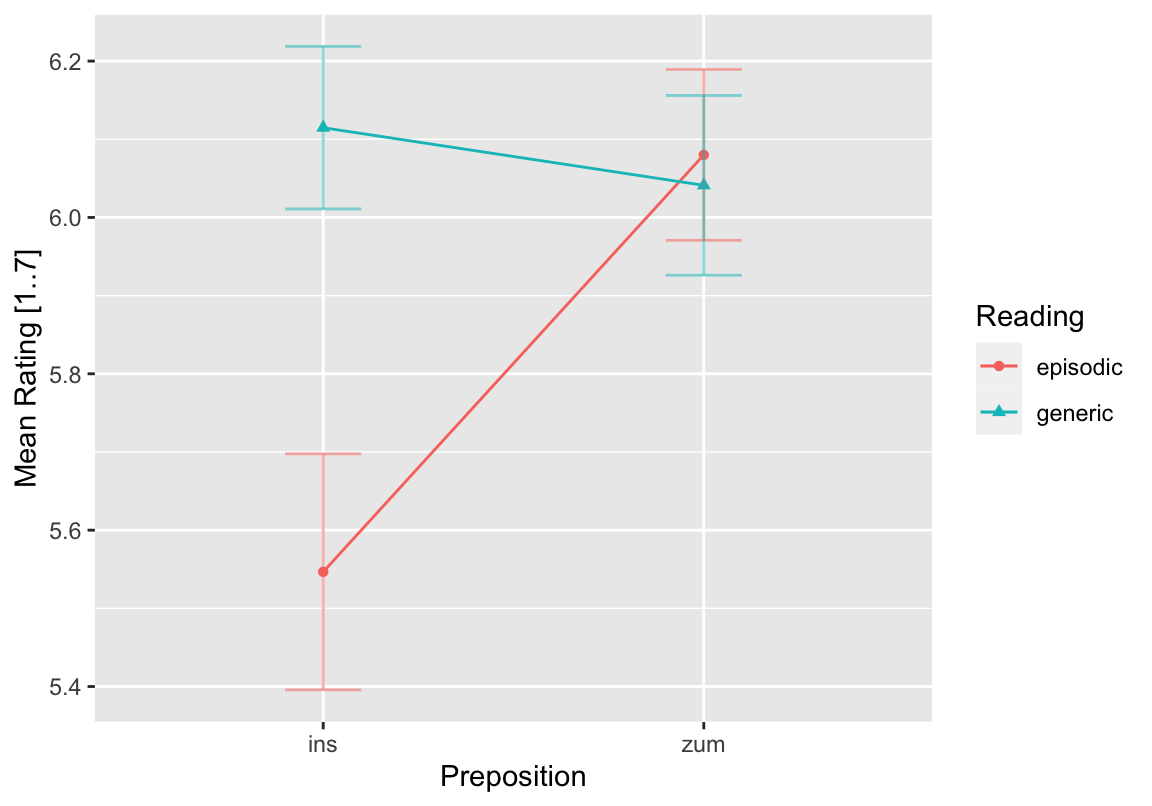
Ein Plot zum Abschluss

library(ggplot2)
p <- ggplot(data = d, aes(y = judgement, x = prep, shape = gen,
  color = gen, group = gen)) +
  stat_summary(fun.y = mean, geom = "line") +
  stat_summary(fun.y = mean, geom = "point") +
  stat_summary(fun.data = mean_se, geom = "errorbar",
    width = 0.2, alpha = .5, linetype = 1) +
  labs(y = "Mean Rating [1..7]", x = "Preposition",
    shape = "Reading", color = "Reading")
## Warning: `fun.y` is deprecated. Use `fun` instead.

## Warning: `fun.y` is deprecated. Use `fun` instead.

Ein Plot zum Abschluss

p

Zum Nachdenken

Wie könnte man das folgende Meme in ein Experiment übersetzen? Wie sähe der Versuchsaufbau und wie die afex-ANOVA dazu aus?

Der Glühwein ruft

Beste Grüße und bis nächste Woche!